Question

12．某校新建的运动场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为1.6米，为安全起见，要装扶手AB及两根与看台底部FG垂直的架杆AD和BC（杆子的底端分别为点D、C，AD=BC=1米，∠DAB约为60°）
（1）求点D与点C的高度差DH；
（2）求所用不绣钢材料的总长度（即AD+AB+BC）．

Answer 1

分析 （1）已知看台有四个台阶组成，由图可看出DH由三个台阶组成，看台的总高度已知，则DH的长不难求得；
（2）过B作BM⊥AH于M，则四边形BCHM是矩形，从而得到BC=MH，再利用三角函数可求得AD，AB的长．那么所用不锈钢材料的总长度l就不难得到了．

解答 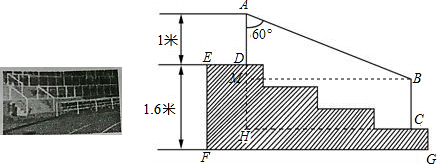解：（1）DH=1.6×$\frac{3}{4}$=1.2（米）；

（2）过B作BM⊥AH于M，则四边形BCHM是矩形．
∴MH=BC=1，
∴AM=AH-MH=1+1.2-1=1.2．
在Rt△AMB中，∠A=60°．
∴AB=$\frac{AM}{cos60°}$=$\frac{1.2}{\frac{1}{2}}$=2.4（米）．
∴l=AD+AB+BC≈1+2.4+1=4.4（米）．
答：点D与点C的高度差DH为1.2米；所用不锈钢材料的总长度约为4.4米．

点评 此题主要考查学生对坡度坡角的理解及解直角三角形的综合运用能力，解题的关键是从实际问题中抽象出直角三角形，难度不大．