
分析 根据例题中的已知的两个式子的关系,两个中二次三项式x2-4x+m的二次项系数是1,因式是(x+3)的一次项系数也是1,利用待定系数法求出另一个因式.所求的式子2x2+3x-k的二次项系数是2,因式是(2x-5)的一次项系数是2,则另一个因式的一次项系数一定是1,利用待定系数法,就可以求出另一个因式.
解答 解:设另一个因式为(x+a),得
2x2+3x-k=(x-5)(x+a)
则2x2+3x-k=2x2+(a-5)x-5a
∴$\left\{\begin{array}{l}{a-5=3}\\{-5a=-k}\end{array}\right.$,
解得:a=8,k=40
故另一个因式为(x+8),k的值为40.
点评 本题考查了因式分解-十字相乘法,正确读懂例题,理解如何利用待定系数法求解是解本题的关键.


科目:初中数学 来源: 题型:解答题
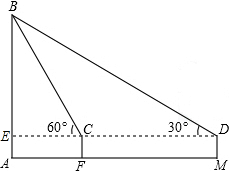 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高.
如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,数轴上表示1、$\sqrt{2}$的对应点为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.
如图所示,数轴上表示1、$\sqrt{2}$的对应点为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
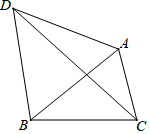 如图所示,△ABC为锐角三角形,以AB为边在△ABC的外边作等边△ABD,连结CD,若△ACD绕着点A逆时针旋转60°,试解答下列问题.
如图所示,△ABC为锐角三角形,以AB为边在△ABC的外边作等边△ABD,连结CD,若△ACD绕着点A逆时针旋转60°,试解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4x<24与x<-6 | B. | 3x≤9与x-3≥0 | ||
| C. | 2x-7<6x与x<-$\frac{7}{4}$ | D. | -$\frac{1}{2}$x+3<0与$\frac{1}{3}$x-2>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com