
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度.已知动点A、B的速度比为1∶3(速度单位:1个单位长度/秒).

(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
【答案】(1)点A的运动速度为2个单位长度/秒,则点B的运动速度为6个单位长度/秒;
(2)点A表示的数是-4,点B表示的数是12;
(3)经过0.4秒或10秒,满足OB=2OA.
【解析】试题分析:(1)设动点A的速度是x单位长度/秒,那么动点B的速度是3x单位长度/秒,然后根据2秒后,两点相距16个单位长度即可列出方程解决问题;
(2)根据(1)的结果和已知条件即可得出.
(3)此问分两种情况讨论:设经过时间为x后,B在A的右边,若A在B的右边,列出等式解出x即可;
解:(1)设动点A的速度是x单位长度/秒,
根据题意得2(x+3x)=16
∴8x=16,
解得:x=2,
则3x=6.
答:动点A的速度是2单位长度/秒,动点B的速度是6单位长度/秒;
(2)标出A,B点如图,
![]() ;
;
(3)设x秒时,OB=2OA,
当B在A的右边,
根据题意得:12﹣6x=2(4+2x),
∴x=0.4,
当A在B的右边,
根据题意得:6x﹣12=2(4+2x),
∴x=10
∴0.4,10秒时OB=2OA.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= ![]() (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1. 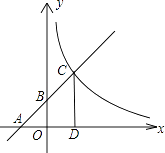
(1)求点A、B、D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形![]() ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形![]() 放到数轴上,如图
放到数轴上,如图![]() ,使得
,使得![]() 与
与![]() 重合,点
重合,点![]() 与
与![]() 重合,点
重合,点![]() 与点
与点![]() 关于
关于![]() 点对称,那么
点对称,那么![]() 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点![]() 在数轴上表示的数为__________.
在数轴上表示的数为__________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州市从![]() 年
年![]() 月
月![]() 日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
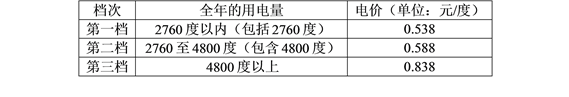
(![]() )小王家
)小王家![]() 年全年的用电量是
年全年的用电量是![]() 度,请计算小王家这年的电费付了多少元?
度,请计算小王家这年的电费付了多少元?
(![]() )小李家
)小李家![]() 年
年![]() 月份这个月的用电量是
月份这个月的用电量是![]() 度,小李算出它们家的电费是
度,小李算出它们家的电费是![]() 元,而供电局却收了小李家的电费
元,而供电局却收了小李家的电费![]() 元,你知道其中的奥秘吗?请你来解释下.
元,你知道其中的奥秘吗?请你来解释下.
(![]() )小张家
)小张家![]() 年全年用电量为
年全年用电量为![]() 度,请用含
度,请用含![]() 的代数式表示小张家全年应交的总电费,并把结果化简.
的代数式表示小张家全年应交的总电费,并把结果化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点B的坐标为(3,4),一次函数 ![]() 的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE上的一个动点.
的图象与边OC、AB分别交于点D、E,并且满足OD=BE.点M是线段DE上的一个动点.
(1)求b的值;
(2)连结OM,若三角形ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成,硬纸板用如图两种方法裁剪(裁剪后边角料不再利用).

现有19张硬纸板,其中x张硬纸板用方法一裁剪,其余硬纸板用方法二裁剪.
(1)分别求裁剪出的侧面和底面的个数.(用含x的代数式表示)
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com