
【题目】已知在△ABC中,AB=AC。

(1)若D为AC的中点,BD把三角形的周长分为24cm和30cm两部分,求△ABC三边的长;
(2)若D为AC上一点,试说明AC>![]() (BD+DC)。
(BD+DC)。
【答案】(1)三角形的三边长为16,16,22或20,20,14;(2)理由见解析
【解析】试题分析:(1)分两种情况讨论:当AB+AD=30,BC+DC=24或AB+AD=24,BC+DC=30,所以根据等腰三角形的两腰相等和中线的性质可求得,三边长为16,16,22或20,20,14;
(2)根据三角形两边之和大于第三边即可得到AC>![]() (BD+DC).
(BD+DC).
试题解析:
(1)设三角形的腰AB=AC=x,
若AB+AD=24cm,
则:x+x=24
∴x=16
三角形的周长为24+30=54cm
所以三边长分别为16,16,22;
若AB+AD=30cm,
则:x+x=30
∴x=20
∵三角形的周长为24+30=54cm
∴三边长分别为20,20,14;
因此,三角形的三边长为16,16,22或20,20,14。
(2)∵AC=AD+CD,AB=AC,
∴2AC=AB+AD+CD>BD+DC,
∴AC>![]() (BD+DC)。
(BD+DC)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个数能否被99整除是从这个数的末位开始,两位一段,看看这些数段的和能否被99整除。像这样能够被99整除的数,我们称之为“长久数”。例如542718,因为18+27+54=99,所以542718能够被99整除;又例如25146,因为46+51+2=99,所以25146能够被99整除。
(1)若![]() 这个三位数是“长久数”,求a的值;
这个三位数是“长久数”,求a的值;
(2)在(1)中的三位数的首位和个位与十位之间加上和为9的两个数字,让其成为一个五位数,该五位数仍是“长久数”,求这个五位数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学表达式:①-2<0; ②3x-5>0; ③ x=1; ④x2-x ;⑤x≠-2 ;⑥x+2>x-1中,不等式有( ).
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形的两边及其中一边的对角对应相等,那么这两个三角形全等,其逆命题是_______________________,这个逆命题是________命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次体育测试中,小芳所在小组8个人的成绩分别是:46,47,48,48,49,49,49,50.则这8个人体育成绩的中位数是( )
A.47B.48C.48.5D.49
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三边长和面积都是整数的三角形称为“整数三角形”.
数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.
小亮用12根火柴棒,摆成如图所示的“整数三角形”;
小颖分别用24根和30根火柴棒摆出直角“整数三角形”;
小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”.

⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;
⑵你能否也从中取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.
①画出等边“整数三角形”;
②摆出一个非特殊(既非直角三角形,也非等腰三角形)“整数三角形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
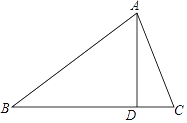
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
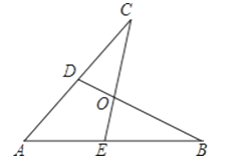
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com