
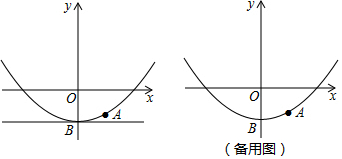
���� ��1�����ô���ϵ�������ɽ�����⣮
��2��ֻҪ֤��Բ��C��ֱ��l�ľ������Բ�İ뾶���ɣ�
��3�������ɣ�2����֪����ֱ��l���C���У���2t-$\frac{5}{8}$=t+$\frac{5}{8}$��t=$\frac{5}{4}$���ɴ˼����жϵ�0��t��$\frac{5}{4}$ʱ��ֱ��l���C�ཻ��
����Ϊ0��t��$\frac{5}{4}$ʱ��Բ��C��ֱ��l�ľ���Ϊd=|2t-$\frac{5}{8}$|���ְ뾶Ϊr=t+$\frac{5}{8}$������a2=4��r2-d2��=4[��t+$\frac{5}{8}$��2-|2t-$\frac{5}{8}$|2]=-12t2+15t�����ݶ��κ��������ʼ��ɽ�����⣮
��� �⣺��1������A��1��-$\frac{3}{4}$������y=$\frac{1}{4}$x2+m�У��ã�
m=-1��
�������ߵĽ���ʽ��y=$\frac{1}{4}$x2-1��
��2�����ۣ�ֱ��l���Cʼ�ձ������У�
���ɣ���P����������루1���Ľ���ʽ���ã�
$\frac{1}{4}$a2-1=-$\frac{3}{4}$+2t��a=$\sqrt{8t+1}$��
��P�� $\sqrt{8t+1}$��-$\frac{3}{4}$+2t����
��Բ��C�� $\frac{\sqrt{8t+1}}{2}$��-$\frac{3}{8}$+t����
���C��ֱ��l�ľ��룺-$\frac{3}{8}$+t-��-1��=t+$\frac{5}{8}$��
��OP2=8t+1+��-$\frac{3}{4}$+2t��2����OP=2t+$\frac{5}{4}$���뾶OC=t+$\frac{5}{8}$��
��ֱ��l���Cʼ�ձ������У�
��3�����ɣ�1����֪����ֱ��l���C���У���2t-$\frac{5}{8}$=t+$\frac{5}{8}$��t=$\frac{5}{4}$��
�൱0��t��$\frac{5}{4}$ʱ��ֱ��l���C�ཻ��
�ڡ�0��t��$\frac{5}{4}$ʱ��Բ��C��ֱ��l�ľ���Ϊd=|2t-$\frac{5}{8}$|���ְ뾶Ϊr=t+$\frac{5}{8}$��
��a2=4��r2-d2��=4[��t+$\frac{5}{8}$��2-|2t-$\frac{5}{8}$|2]=-12t2+15t��
��t=$\frac{5}{8}$ʱ��a��ƽ��ȡ�����ֵΪ $\frac{75}{16}$��
���� ���⿼����κ����ۺ��⡢ֱ����Բ��λ�ù�ϵ��֪ʶ������Ĺؼ����������ֱ����Բ���е��ж��������ڴ�����������ʱ��Ҫע��Ѱ�ҹؼ����Լ��ֶν������ۣ��������©�⣮


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017������ʡ�����о��꼶��һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ���ѡ��
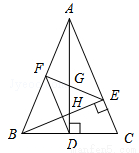
��ͼ���ڡ�ABC�У�AD��BE�Ǹߣ���ABE=45�㣬��F��AB���е㣬AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE����AH=2CD����BC•AD=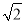 AE2���ܡ�DFE=2��DAC ;��������CH����CH��EF.������ȷ�ĸ���Ϊ�� ��
AE2���ܡ�DFE=2��DAC ;��������CH����CH��EF.������ȷ�ĸ���Ϊ�� ��
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
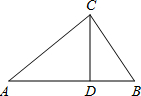 ��ͼ����Rt��ABC�У�CD��б��AB�ϵĸߣ���BD=4��CD=6����AD�ij�Ϊ��������
��ͼ����Rt��ABC�У�CD��б��AB�ϵĸߣ���BD=4��CD=6����AD�ij�Ϊ��������| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | C��r | B�� | C����r | C�� | C���� | D�� | C��2��r |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��AC=8��BD=6�������εı߳�AB=5��
��ͼ��������ABCD�У�AC��BD�ཻ�ڵ�O��AC=8��BD=6�������εı߳�AB=5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com