
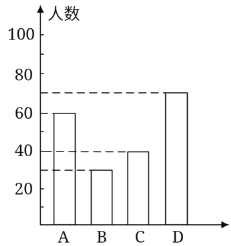
����Ŀ��ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ���ѧϰʱ������������ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ�����ѧϰʱ��Ϊt��Сʱ����A��t��1��B��1��t��1.5��C��1.5��t��2��D��t��2�����ݵ�������������ͼ��ʾ��������������ͳ��ͼ��

�������ͼ����Ϣ����������⣺
��1�����γ������鹲��ȡ��____��ѧ������������ͳ��ͼ����������
��2�����γ��������У�ѧϰʱ�����λ������____�ȼ��ڣ�
��3����ʾB�ȼ�������Բ�Ľ����Ķ�����_____�㣮
���𰸡���1��200����2��C����3��54��
��������
��1�����ݵȼ�A����������ռ�İٷֱȿ��������������ȼ�C�������Ӷ���ȫ����ͼ��
��2��������λ���Ķ��弴�ɵõ�200��ѧ������λ������C�ȼ���
��3����B�ȼ������������������ٳ���360�㣬���ɵõ�Բ�ĽǶ�����
�⣺��������ͳ��ͼ������ͳ��ͼ��֪���ȼ�A����60�ˣ�ռ������30����
�����������������![]() ���ˣ�
���ˣ�
��ȼ�C��������![]() ���ˣ�
���ˣ�
��ȫ����ͼ����ͼ��ʾ��
��2����Ϊ����200�˽��ܵ��飬������λ���Ķ����֪��ѧϰʱ�����λ���ڵȼ�C�ڣ�
��3����������ɵã�![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
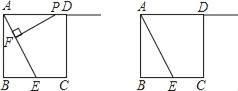
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4��E��BC�ߵ��е㣬��P������AD�ϣ���P��PF��AE��F����PA��x��
(1)��֤����PFA�ס�ABE��
(2)����P��F��EΪ�����������Ҳ���ABE���ƣ�����x��ֵ��
(3)����xȡ��ֵʱ����DΪԲ�ģ�DPΪ�뾶�ġ�D���߶�AEֻ��һ�������㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
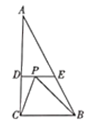
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ��һ���㣮����
��һ���㣮����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ������������
������������![]() ����
����![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪�����������θ��߶����е�Բ���������ε�����Բ���������ο��Գ�ΪԲ�����������Σ���ͼ1��![]() ��
��![]() ������
������![]() �ֱ������ڵ�
�ֱ������ڵ�![]() ��
��![]() ����
����![]() ������������.�Դ����ƣ����߶���Բ���е��ı��γ�ΪԲ�����ı��Σ���ͼ2��
������������.�Դ����ƣ����߶���Բ���е��ı��γ�ΪԲ�����ı��Σ���ͼ2��![]() ���ı���ABCD�ı�
���ı���ABCD�ı�![]() �ֱ������ڵ�
�ֱ������ڵ�![]() ���ı���
���ı���![]() ����
����![]() �������ı��Σ�
�������ı��Σ�
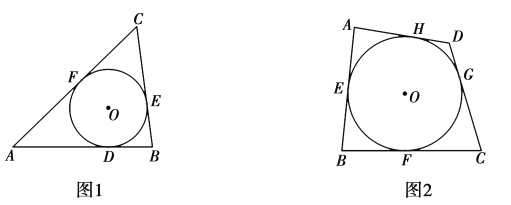
��1����ͼ2����̽��Բ�����ı���![]() ������Ա�
������Ա�![]() ��
��![]() ֮���������ϵ�����룺
֮���������ϵ�����룺![]()
![]() (����������>������<������=��)��
(����������>������<������=��)��
��2������ͼ2֤����IJ���(д����֪����֤��֤������)��
��3����������������֤���Ľ��ۣ� ��
��4����Բ�����ı��ε��ܳ�Ϊ![]() ���ڵ������ߵı�Ϊ
���ڵ������ߵı�Ϊ![]() ������ı��θ��ߵij���
������ı��θ��ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
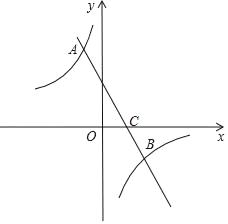
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y=![]() ��m��0�����ڵ�A����
��m��0�����ڵ�A����![]() ��2����B��n����1����
��2����B��n����1����
��1����ֱ����˫���ߵĽ���ʽ��
��2����P��x���ϣ����S��ABP=3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й��ں���![]() ���ĸ����⣺
���ĸ����⣺
�ٵ�x=0ʱ��y����Сֵ12��
��nΪ����ʵ����x=3+nʱ�ĺ���ֵ����x=3-nʱ�ĺ���ֵ��
����n��3����n����������![]() ʱ��y������ֵ��
ʱ��y������ֵ��![]() ����
����
��������ͼ�����![]() ��
��![]() ������a��0��b��0����a��b��
������a��0��b��0����a��b��
���������������ǣ�������
A.��B.��C.��D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD���ĸ����㶼��˫����y��![]() ��k��0���ϣ�BC��2AB���Ҿ���ABCD�������32����k��ֵ�ǣ� ��
��k��0���ϣ�BC��2AB���Ҿ���ABCD�������32����k��ֵ�ǣ� ��
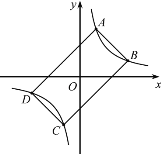
A.6B.8C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
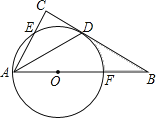
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬��BAC��ƽ���߽�BC�ڵ�D����O��AB�ϣ��Ե�OΪԲ�ģ�OAΪ�뾶��Բǡ�þ�����D���ֱ�AC��AB�ڵ�E��F��
��1�����ж�ֱ��BC����O��λ�ù�ϵ����˵�����ɣ�
��2����BD��2![]() ��BF��2������Ӱ���ֵ�������������������
��BF��2������Ӱ���ֵ�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
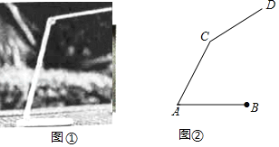
����Ŀ��ͼ���Ƿ�����ˮƽ���ϵ�̨�ƣ�ͼ���������ʾ��ͼ��̨�Ƶ����߶Ⱥ��Բ��ƣ������еƱ�AC��44cm������CD��32cm���Ʊ���������ɵġ�CAB��60����CD�����Ƶ�C���µ���һ���ĽǶȣ�ʹ�÷��֣���CD��ˮƽ�����ɵĽ�Ϊ30��ʱ��̨�ƹ�����ѣ��ֲ�õ�D������ľ���Ϊ54.06cm����ͨ������˵����ʱ̨�ƹ����Ƿ�Ϊ��ѣ����ο����ݣ�![]() ȡ1.73����
ȡ1.73����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com