
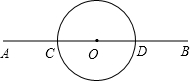
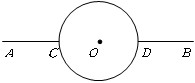
 如图,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A、B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→弧CD→线段DB,其中C、D在直线AB上.则最短的行走路线的长度是
如图,在相距60km的两个城镇A,B之间,有一近似圆形的湖泊,其半径为15km,圆心O恰好位于A、B连线的中点处.现要绕过湖泊从A城到B城,假设除湖泊外,所有的地方均可行走,如路线:线段AC→弧CD→线段DB,其中C、D在直线AB上.则最短的行走路线的长度是科目:初中数学 来源: 题型:
 |
| CD |
 B上.请你找出最短的行走路线,并求出这条路线的长度.(
B上.请你找出最短的行走路线,并求出这条路线的长度.(| 3 |
查看答案和解析>>
科目:初中数学 来源:鄂尔多斯 题型:解答题
 |
| CD |
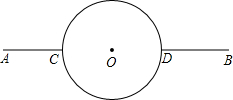
| 3 |
查看答案和解析>>
科目:初中数学 来源:内蒙古自治区中考真题 题型:解答题
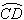 →线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度。
→线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度。
查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》中考题集(68):5.8 弧长及扇形的面积(解析版) 题型:解答题
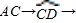 线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.(
线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.( ≈1.73,π≈3.14)
≈1.73,π≈3.14)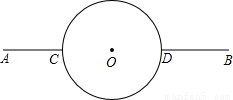
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com