
【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?

科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C(0,4),射线CE∥x轴,直线y=﹣ ![]() x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 .
x+b交线段OC于点B,交x轴于点A,D是射线CE上一点.若存在点D,使得△ABD恰为等腰直角三角形,则b的值为 . 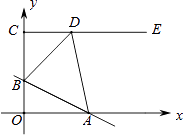
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE. 
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级(1)班去体育用品商店买一些篮球和排球,供班上同学阳光体育课间使用,共买了3个篮球和5个排球,花570元,并且每个排球比篮球便宜30元.
(1)求篮球和排球的单价各是多少吗?
(2)商店里搞活动,有两种套餐,①套装打折:五个篮球和五个排球为一套装,套装打八折;②满减活动:999减100,1999减200;两种活动不重复参与,学校打算买15个篮球,13个排球作为奖品,请问如何安排更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).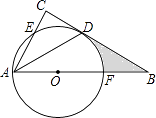
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1 , 0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )
A.a(x1﹣x2)=d
B.a(x2﹣x1)=d
C.a(x1﹣x2)2=d
D.a(x1+x2)2=d
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com