
【题目】已知抛物线y=x2﹣mx﹣3与直线y=2x+3m在﹣2<x<2之间有且只有一个公共点,则m的取值范围是_____
【答案】![]() ≤m<5或m=﹣8+4
≤m<5或m=﹣8+4![]()
【解析】
根据二次函数图象与系数之间的关系即可求出答案.
联立 可得:x2﹣(m+2)x﹣3m﹣3=0,
可得:x2﹣(m+2)x﹣3m﹣3=0,
令y=x2﹣(m+2)x﹣3m﹣3=0,
∴抛物线y=x2﹣mx﹣3与直线y=x+3m在﹣2<x<2之间有且只有一个公共点,
即y=x2﹣(m+2)x﹣3m﹣3=0的图象在﹣2<x<2上只有一个交点,
当△=0时,
即△=(m+2)2﹣4(﹣3m﹣3)=0,
解得:m=﹣8±4![]() ,
,
当m=﹣8+4![]() 时,
时,
x=![]() =﹣3+2
=﹣3+2![]() ,满足题意,
,满足题意,
当m=﹣8﹣4![]() 时,
时,
x=![]() =﹣3﹣2
=﹣3﹣2![]() <﹣2,
<﹣2,
当△>0,
∴令x=﹣2,y=﹣m+5,
令x=2,y=﹣5m﹣3,
∴(﹣m+5)(﹣5m﹣3)<0,
∴﹣![]() <m<5,
<m<5,
当x=2时,代入x2﹣(m+2)x﹣3m﹣3=0,
解得m=﹣![]() ,
,
∴方程的另一根是﹣![]() ,符合题意,
,符合题意,
故m的取值范围为:﹣![]() ≤m<5或m=﹣8+4
≤m<5或m=﹣8+4![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形![]() 的边
的边![]() 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为![]() 顺次连接这四个点,得四边形
顺次连接这四个点,得四边形![]() .
.
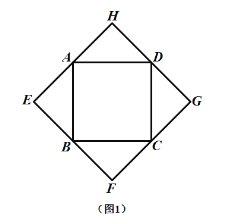
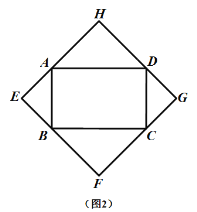
(1)如(图1).当四边形![]() 为正方形时,我们发现四边形
为正方形时,我们发现四边形![]() 是正方形;如(图2),当四边形
是正方形;如(图2),当四边形![]() 为矩形时,请判断:四边形
为矩形时,请判断:四边形![]() 的形状(不要求证明);
的形状(不要求证明);
(2)如(图3),当四边形![]() 为一般平行四边形时 ,设
为一般平行四边形时 ,设![]()
①试用含![]() 的代数式表示
的代数式表示![]() ;
;
②求证:四边形![]() 是正方形,
是正方形,
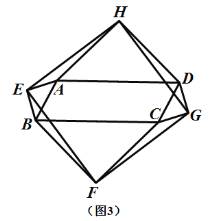
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
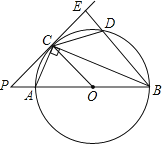
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
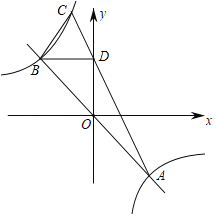
【题目】如图,反比例函数y=![]() (k≠0)与直线交于A,B两点.
(k≠0)与直线交于A,B两点.
(1)求证:OB=OA;
(2)连接CA交y轴于D点BD∥x轴,判断CB,CD的数量关系;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机抽取了九年级部分学生进行体育模拟测试,将成绩统计分析并绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,绘制成如下所示的两幅统计图表(不完整的)
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |

请你根据图表中的信息完成下列问题:
(1)本次抽样调查的样本容量是 ,其中m= ,n= ;
(2)扇形统计图中E等级对应扇形的圆心角α= °;
(3)已知该校九年级共有700名学生,可以估计体育测试成绩在A、B两个等级的人数共有 人;
(4)该校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中随机选择2名作为代表参加全市体育交流活动,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com