
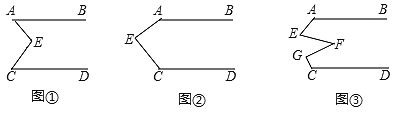
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
【答案】【感知】见解析;【探究】∠BAE+∠AEC+∠DCE=360°;【应用】396°.
【解析】
感知:如图①,过点E作EF∥AB.利用平行线的性质即可解决问题;
探究:如图2中,作EG∥AB,利用平行线的性质即可解决问题;
应用:作FH∥AB,利用平行线的性质即可解决问题;
解:理由如下,
【感知】
过E点作EF//AB
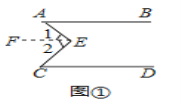
∵AB//CD
∴EF//CD
∵AB//CD
∴∠BAE=∠AEF
∵EF//CD
∴∠CEF=∠DCE
∴∠BAE+∠DCE=∠AEC.
【探究】
过E点作AB//EG.
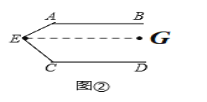
∵AB//CD
∴EG//CD
∵AB//CD
∴∠BAE+∠AEG=180°
∵EG//CD
∴∠CEG+∠DCE=180°
∴∠BAE+∠AEC+∠DCE=360°
【应用】
过点F作FH∥AB.
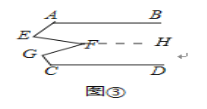
∵AB∥CD,
∴FH∥CD,
∴∠BAE+∠AEF+∠EFH=360°,∠HFG+∠FGC+∠GCD=360°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD=720°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD+∠EFG=720°+36°,
∴∠BAE+∠AEF+∠FGC+∠DCG=720°-360°+36°=396°
故答案为:396°.


科目:初中数学 来源: 题型:
【题目】如图,数轴正半轴上的![]() ,
,![]() 两点分别表示有理数
两点分别表示有理数![]() ,
,![]() ,
,![]() 为原点,若
为原点,若![]() ,线段
,线段![]() .
.

(1)![]() ______,
______,![]() ______;
______;
(2)若点![]() 从点
从点![]() 出发,以每秒2个单位长度向
出发,以每秒2个单位长度向![]() 轴正半轴运动,求运动时间为多少时;点
轴正半轴运动,求运动时间为多少时;点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 距离的3倍;
距离的3倍;
(3)数轴上还有一点![]() 表示的数为32,若点
表示的数为32,若点![]() 和点
和点![]() 同时从点
同时从点![]() 和点
和点![]() 出发,分别以每秒2个单位长度和每秒1个单位长度的速度向
出发,分别以每秒2个单位长度和每秒1个单位长度的速度向![]() 点运动,
点运动,![]() 点到达
点到达![]() 点后,再立刻以同样的速度返回,运动到终点
点后,再立刻以同样的速度返回,运动到终点![]() ,求点
,求点![]() 和点
和点![]() 运动多少秒时,
运动多少秒时,![]() 、
、![]() 两点之间的距离为4.
两点之间的距离为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
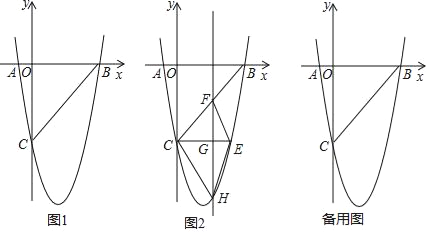
【题目】如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次活动课上,第一小组同学把一个边长为1正方形纸片按如图方法剪裁:第一次剪成四个大小形状一样的小正方形,第二次将其中的一个小正方形再按向样的方法剪成四个小正方形,第三次再按同样的方法将其中一个小正方形剪成四个小正方形,如此循环进行下去.请你替他们完成下列问题:
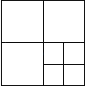
(1)完成表格:
剪的次数 | 1 | 2 | 3 | 4 | 5 | … |
正方形 个数 |
|
| 10 |
|
| … |
(2)如果剪了100次,共剪出 个小正方形;
(3)如果剪了n次,共剪出 个小正方形;
(4)如果剪了n次,则第n次得到的正方形边长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
的图象交于A,B两点.当一次函数的值大于反比例函数的值时,自变量x的取值范围是( )
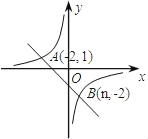
A. ﹣2<x<1 B. 0<x<1 C. x<﹣2和0<x<1 D. ﹣2<x<1和x>1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
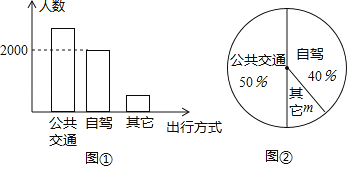
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A在原点左侧,点B在原点右侧,且点A到原点的距离是点B到原点距离的2倍,AB=15.
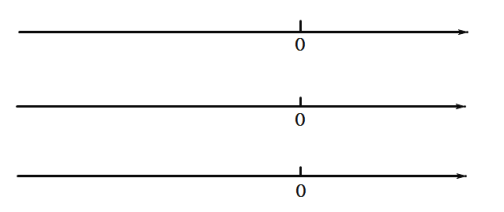
(1)点A表示的数为________,点B表示的数为________;
(2)点P从点A出发,以每秒1个单位长度的速度向点B方向运动;同时,点Q从点B出发,先向点A方向运动,当与点P重合后,马上改变方向与点P同向而行且速度始终为每秒2个单位长度。设运动时间为t秒。
①当点P与点Q重合时,求t的值;
②当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习千万条,思考第一条。请你用本学期所学知识探究以下问题:
(1)已知点![]() 为直线
为直线![]() 上一点,将直角三角板
上一点,将直角三角板![]() 的直角顶点放在点
的直角顶点放在点![]() 处,并在
处,并在![]() 内部作射线
内部作射线![]() .
.
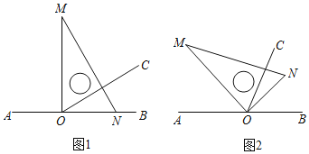
①如图1,三角板的一边![]() 与射线
与射线![]() 重合,且
重合,且![]() ,若以点
,若以点![]() 为观察中心,射线
为观察中心,射线![]() 表示正北方向,求射线
表示正北方向,求射线![]() 表示的方向;
表示的方向;
②如图2,将三角板放置到如图位置,使![]() 恰好平分
恰好平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
(2)已知点![]() 不在同一条直线上,
不在同一条直线上,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,用含
,用含![]() 的式子表示
的式子表示![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com