
【题目】四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
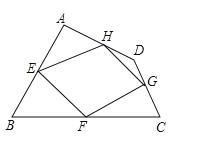
(1)四边形EFGH的形状是什么,并证明你的结论.
(2)当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形;并利用你给的条件加以证明.
【答案】(1)平行四边形;(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
【解析】
(1)连接AC和BD,根据中位线知识得EH∥FG,EF∥HG,从而证明四边形EFGH为平行四边形;
(2)当AC⊥BD时,可证EH⊥HG,从而证明四边形EFGH为矩形.
解:(1)连接AC,BD,
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,FG∥BD,HG∥AC,EF∥AC,
∴EH∥FG,,EF∥HG,
∴四边形EFGH是平行四边形;
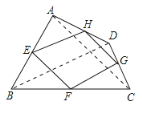
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形,理由如下:
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,FG∥BD,HG∥AC,EF∥AC,
∴EH∥FG,,EF∥HG,
∴四边形EFGH是平行四边形,
∵AC⊥BD,
∴EH⊥HG,
∴平行四边形EFGH是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,受疫情影响,电脑价格不断下降,今年四月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的甲种电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年四月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再进销售价为6000元的乙种型号电脑,四月份甲、乙两种电脑共销售15台,如果销售额不低于8万元,则乙种型号电脑销售不低于多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
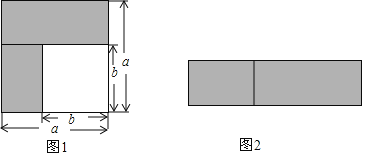
小题1:如图1,可以求出阴影部分的面积是_______ (写成两数平方差的形式);
小题2:如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是_______,长是______,面积是_________ (写成多项式乘法的形式).
小题3:比较图 1,图2的阴影部分面积,可以得到乘法公式________ (用式子表达).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,数学来源于生活又服务于生活,利用数学中的知识可以帮助我们解决许多实际问题.如王明想建一个超市,经调查发现他家附近有两个大的居民区![]() ,
,![]() ,同时又有相交的两条公路
,同时又有相交的两条公路![]() ,
,![]() ,为方便进货和居民生活,王明想把超市建在到两居民区的距离相等,同时到两公路距离也相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助王明在图上确定超市的位置!请用尺规作图确定超市点
,为方便进货和居民生活,王明想把超市建在到两居民区的距离相等,同时到两公路距离也相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助王明在图上确定超市的位置!请用尺规作图确定超市点![]() 的位置.(作图不写作法,但要求保留作图痕迹)
的位置.(作图不写作法,但要求保留作图痕迹)
先将实际问题转化为数学问题,把超市看作一个点.
点![]() 到
到![]() ,
,![]() 两点的距离相等,根据性质:__________________, 需用尺规作出_____________;又点
两点的距离相等,根据性质:__________________, 需用尺规作出_____________;又点![]() 到两相交直线
到两相交直线![]() ,
,![]() 的距离相等,根据性质:_________________, 需用尺规作出_______________;而点
的距离相等,根据性质:_________________, 需用尺规作出_______________;而点![]() 同时满足上述两个条件,因此应该是它们的交点.
同时满足上述两个条件,因此应该是它们的交点.
请同学们先完成分析过程(即填空) ,再作图;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
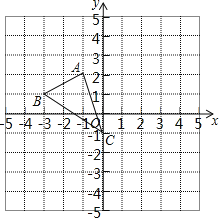
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com