
已知:抛物线y=-![]() x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
x2-(m+3)x+m2-12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.

(1)求抛物线的解析式;
(2)在x轴上,点A的左侧,求一点E,使△ECO与⊙CAO相似,并说明直线EC经过(1)中抛物线的顶点D;
(3)过(2)中的点E的直线y=![]() x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为
x+b与(1)中的抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为![]() 、
、![]() ,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形MM'NN':S△QMN=35∶12,若存在,求出满足条件的t值;若不存在,请说明理由.
,点P为线段MN上一点,点P的横坐标为t,过点P作平行于y轴的直线交(1)中所求抛物线于点Q.是否存在t值,使S梯形MM'NN':S△QMN=35∶12,若存在,求出满足条件的t值;若不存在,请说明理由.
|
(1)∵x1<0,x2>0,∴OA=-x1,OB=x2,∵x1,x2是方程- (2)设点E(x,0),则OE=-x,∵△ECO与△CAO相似,∴ 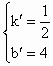 ,所以直线CE的解析式y= ,所以直线CE的解析式y=(3)存在t值,使S梯形MM′N′N∶S△QMN=35∶12.∵E(-8,0),∴0= 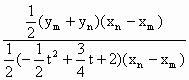 = = |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:江西省高安市2012届九年级第一次模拟考试数学试题 题型:044
已知:抛物线y=a(x-2)2+b(ab<0)的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请求出a,b满足的关系式;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=![]() x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).
1.求抛物线的解析式
2.设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得![]() ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由
3.射线OC上有两个动点P、Q同时从原点出发,分别以每秒![]() 个单位长度、每秒2
个单位长度、每秒2![]() 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源:2012届北京石景山中考二模数学试卷(带解析) 题型:解答题
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=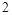 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).
【小题1】求抛物线的解析式
【小题2】设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得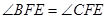 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由
【小题3】射线OC上有两个动点P、Q同时从原点出发,分别以每秒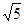 个单位长度、每秒2
个单位长度、每秒2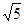 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京石景山中考二模数学试卷(解析版) 题型:解答题
已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线
y=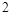 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).
1.求抛物线的解析式
2.设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得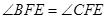 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由
3.射线OC上有两个动点P、Q同时从原点出发,分别以每秒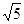 个单位长度、每秒2
个单位长度、每秒2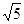 个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ(直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com