
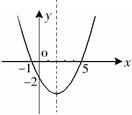
 时x的值只能取0
时x的值只能取0| A.1个 | B.2个 | C.3个 | D.4个 |
 每课必练系列答案
每课必练系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中,  , 高
, 高 (如图1). 动点
(如图1). 动点 同时从点
同时从点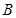 出发, 点
出发, 点 沿
沿 运动到点
运动到点 停止, 点
停止, 点 沿
沿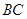 运动到点
运动到点 停止,两点运动时的速度都是1cm/s,而当点
停止,两点运动时的速度都是1cm/s,而当点 到达点
到达点 时,点
时,点 正好到达点
正好到达点 . 设
. 设 同时从点
同时从点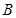 出发,经过的时间为
出发,经过的时间为 (s)时,
(s)时,  的面积为
的面积为 (如图2). 分别以
(如图2). 分别以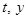 为横、纵坐标建立直角坐标系, 已知点
为横、纵坐标建立直角坐标系, 已知点 在
在 边上从
边上从 到
到 运动时,
运动时,  与
与 的函数图象是图3中的线段
的函数图象是图3中的线段 .
.
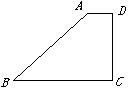

 的长度;
的长度; 在
在 边上和
边上和 边上运动时,
边上运动时,  与
与 的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中
的函数关系式(注明自变量的取值范围), 并在图3中补全整个运动中 关于
关于 的函数关系的大致图象.
的函数关系的大致图象.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
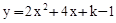 (k为正整数).
(k为正整数).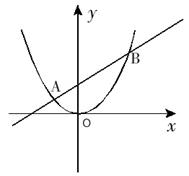
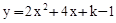 的图象与x轴有两个交点,求k的值.
的图象与x轴有两个交点,求k的值.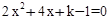 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数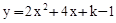 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
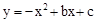 与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.
与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.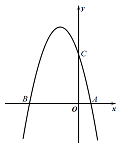
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
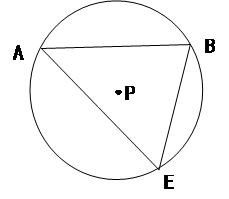
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
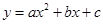 图像的一部分,其对称轴是
图像的一部分,其对称轴是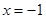 ,且过点(-3,0),下列说法:①
,且过点(-3,0),下列说法:①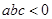 ②
②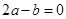 ③
③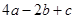 <0 ④若(-5,y1),(1,y2)是抛物线上两点,则
<0 ④若(-5,y1),(1,y2)是抛物线上两点,则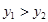 ,其中说法正确的是( )
,其中说法正确的是( )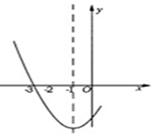
| A.①② | B.②③ | C.①②④ | D.①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com