
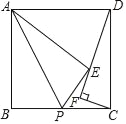
【题目】如图,在正方形ABCD中,P是BC的中点,把△PAB沿着PA翻折得到△PAE,过C作CF⊥DE于F,若CF=2,则DF=_____.
【答案】6.
【解析】
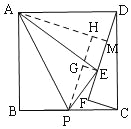
作辅助线,构建全等三角形,证明△AMD≌△DFC,则DM=FC=2,由折叠和正形
的边长相等得:AE=AD,根据等腰三角形三线合一得:DM=EM=2,∠EAM=∠MAD,设∠
MAD=α,则∠EAM=α,∠BAP=∠PAE=45°﹣α,可得∠PAM=45°,则△PAH是等腰直角三
角形,证明△PGE∽△AMD,列比例式得:GE=1,AM=2PG,设PG=x,则AM=2x,根据
AH=PH,得2x﹣1=2+x,求得x的值,即可解决问题;
过A作AM⊥DF于M,
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
∴∠ADF+∠FDC=90°,
∵∠ADF+∠MAD=90°,
∴∠FDC=∠MAD,
∵∠AMD=∠DFC=90°,
∴△AMD≌△DFC,
∴DM=FC=2,
由折叠得:AB=AE,BP=PE,
∵AB=AD,
∴AE=AD,
∴DM=EM=2,∠EAM=∠MAD,
∵P是BC的中点,
∴PC=![]() BC=
BC=![]() AD=PE,
AD=PE,
设∠MAD=α,则∠EAM=α,∠BAP=∠PAE=45°﹣α,
∴∠APE=90°﹣(45°﹣α)=45°+α,
∵∠EAM=∠DAM,∠BAP=∠PAE,
∴∠PAE+∠EAM=![]() ∠BAD=45°,
∠BAD=45°,
过P作PH⊥AM于H,过E作EG⊥PH于G,
∴△PAH是等腰直角三角形,
∴∠APH=45°,
∴∠HPE=α=∠MAD,
∵∠PGE=∠AMD=90°,
∴△PGE∽△AMD,
∴![]()
∴![]()
∴GE=1,AM=2PG,
设PG=x,则AM=2x,
∴AH=2x﹣1,
∵AH=PH,
∴2x﹣1=2+x,
x=3,
∴PG=3,AM=6,
∵△DAM≌△CDF,
∴DF=AM=6.
故答案为:6.


科目:初中数学 来源: 题型:
【题目】(1)解方程:![]() ;
;
(2)列分式方程解应用题:
用电脑程序控制小型赛车进行![]() 比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差
比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差![]() .从赛后数据得知两车的平均速度相差
.从赛后数据得知两车的平均速度相差![]() .求“畅想号”的平均速度.
.求“畅想号”的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
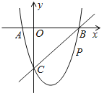
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 点在原点的左侧,
点在原点的左侧,![]() 点的坐标为
点的坐标为![]() ,与
,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 是直线
是直线![]() 下方的抛物线上一动点.
下方的抛物线上一动点.
![]() 求这个二次函数的表达式.
求这个二次函数的表达式.
![]() 连接
连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点
,那么是否存在点![]() ,使四边形
,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 当点
当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 的面积最大?求出此时
的面积最大?求出此时![]() 点的坐标和四边形
点的坐标和四边形![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
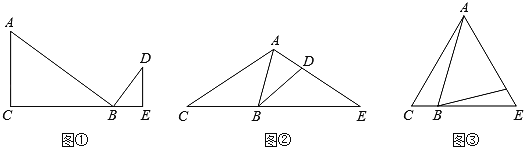
【题目】已知,点B在线段CE上.
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
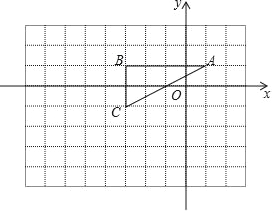
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1),B(﹣3,1),C(﹣3,﹣1).
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_____,⊙P的半径为_____;
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A'、B'、C'.①画出△A'B'C';②将△A'B'C'沿x轴方向平移,需平移_____个单位长度,能使得B'C'所在的直线与⊙P相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
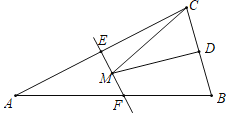
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
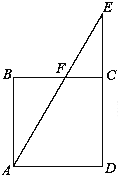
【题目】如图,ABCD是正方形场地,点E在DC的延长线上,AE与BC相交于点F,有甲、乙、丙三名同学同时从点A出发,甲沿着A﹣B﹣F﹣C的路径行走至C,乙沿着A﹣F﹣E﹣C﹣D的路径行走至D,丙沿着A﹣F﹣C﹣D的路径行走至D,若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是( )
A.甲乙丙B.甲丙乙C.乙丙甲D.丙甲乙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com