
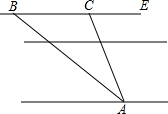
 在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 作AD⊥BE于点D,设AD=x米,在△ACD中CD=$\frac{AD}{tan∠ACD}$=$\frac{\sqrt{3}}{3}$x,在RT△ABD中根据tan∠ABD=$\frac{AD}{BD}$列出关于x的方程,解方程可得x的值,即可知高速公路宽.
解答 解:过点A作AD⊥BE于点D,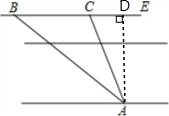
设AD=x米,
在△ACD中,∵∠ACD=60°,tan∠ACD=$\frac{AD}{CD}$,
∴CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$x(m),
在RT△ABD中,∵∠ABD=30°,tan∠ABD=$\frac{AD}{BD}$,
∴$\frac{\sqrt{3}}{3}$=$\frac{x}{8+\frac{\sqrt{3}}{3}x}$,
解得:x=4$\sqrt{3}$,
∴高速公路的宽为4$\sqrt{3}$-1≈6(米),
答:此高速公路的宽约为6米.
点评 本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
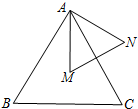 如图,△ABC和△AMN都是等边三角形,点M是△ABC的重心,那么$\frac{{S}_{△AMN}}{{S}_{△ABC}}$的值为( )
如图,△ABC和△AMN都是等边三角形,点M是△ABC的重心,那么$\frac{{S}_{△AMN}}{{S}_{△ABC}}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com