
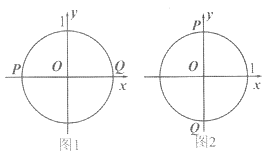
【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.
(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______
(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
【答案】(1)36;(2)①1; ②2;(3)测度面积S的取值范围是18≤S≤![]() .
.
【解析】试题分析:(1)先求出抛物线与直线的交点坐标,再求出抛物线的顶点坐标,然后根据定义进行计算即可得;
(2)①根据给出的定义可以求出来;
②根据定义可以求出测度面积的最大值为2;
(3)因为平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上,注意分三种情况讨论.
试题解析:(1)解方程组![]() 得:
得: ![]() ,
, ![]() ,
,
抛物线y=-x2+2x+3=-(x-1)2+4,
根据定义可知图形W中|x1-x2|的最大值为4,|y1-y2|的最大值为9,则S=4×9=36,
故答案为:36;
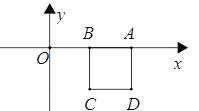
(2)①当A、B都在x轴上时,如图所示,横坐标差的绝对值的最大值为1,纵坐标差的绝对值的最大值为1,根据定义可知图形的测度面积为1,
故答案为:1;
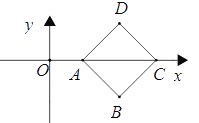
②如图所示摆放时,图形的测度面积最大,
此时横坐标差的绝对值的最大值为![]() ,纵坐标差的绝对值的最大值为
,纵坐标差的绝对值的最大值为![]() ,根据定义可知图形的测度面积为2,
,根据定义可知图形的测度面积为2,
故答案为2;
(3)不妨设矩形ABCD的边AB=6,BC=3. 由已知可得,平移图形W不会改变其测度面积S的大小,将矩形ABCD的其中一个顶点B平移至x轴上. 当顶点A,B或B,C都在x轴上时,如图1和图2,矩形ABCD的测度面积S就是矩形ABCD的面积,此时S=18.
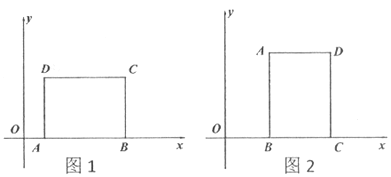
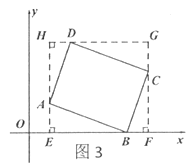
当顶点A,C都不在x轴上时,如图3.
过A作直线AE⊥x轴于点E,过C作直线CF⊥x轴于点F,过D作直线GH∥x轴,与直线AE,CF分别交于点H和点G,则可得四边形EFGH是矩形.
当点P,Q分别与点A,C重合时,|x1-x2|取得最大值m,且最大值m=EF;
当点P,Q分别与点B,D重合时,|y1-y2|取得最大值n,且最大值n=GF.
∴图形W的测度面积S=EF·GF.
∵∠ABC=90°,
∴∠ABE+∠CBF=90°.
∵∠AEB=90°,
∴∠ABE+∠BAE=90°.
∴∠BAE=∠CBF.
又∵∠AEB=∠BFC=90°,
∴△ABE∽△BCF.
∴![]() .
.
设AE=2a,EB=2b(a>0,b>0),则BF=a,FC=b,
在Rt△ABE中,由勾股定理得AE2+BE2=AB2.
∴4a2+4b2=36. 即a2+b2=9.
∵b>0,∴b=![]()
易证△ABE≌△CDG. ∴CG=AE=2a.
∴EF=EB+BF=2b+a,GF=FC+CG=b+2a.
∴S=EF·GF=(2b+a)(b+2a)=2a2+2b2+5ab=18+5a![]()
=18+5![]() =18+5
=18+5![]() =18+5
=18+5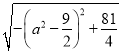
∴当a2=![]() ,即a=
,即a=![]() 时,测度面积S取得最大值18+5×
时,测度面积S取得最大值18+5×![]() =
=![]() .
.
∵a>0,b>0,∴ ![]() . ∴S>18.
. ∴S>18.
∴当顶点A,C都不在x轴上时,S的范围为l8<S≤![]() .
.
综上所述,测度面积S的取值范围是18≤S≤![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:![]() .
.
解:讨论:①当![]() ≥0时,原方程可化为
≥0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
②当![]() <0时,原方程可化为
<0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
∴原方程的解为![]() 和
和![]() .
.
问题(1):依例题的解法,方程![]() 的解是 ;
的解是 ;
问题(2):尝试解绝对值方程:![]() ;
;
问题(3):在理解绝对值方程解法的基础上,解方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
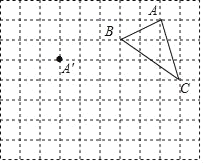
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
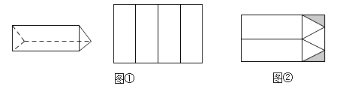
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】指出下列问题中的总体、个体、样本:
(1)为了估计某块玉米试验田里的单株平均产量,从中抽取![]() 株进行实测;
株进行实测;
(2)某学校为了了解学生完成课外作业的时间,从中抽样调查了![]() 名学生完成课外作业的时间进行分析.
名学生完成课外作业的时间进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com