
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上 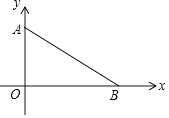
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y= ![]() 的图象经过点M,且sin∠OAB=
的图象经过点M,且sin∠OAB= ![]() ,求k的值.
,求k的值.
【答案】
(1)解:点M为所求作;
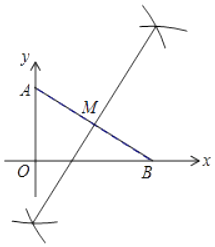
(2)解:∵sin∠OAB= ![]() ,
,
∴设OB=4x,AB=5x,
∴由勾股定理可知:32+(4x)2=(5x)2,
∴x=1,
∴OB=4,
由作图可知M为AB的中点,
∴M(2, ![]() ),
),
将M的坐标代入y= ![]() 中,
中,
∴k=2× ![]() =3,
=3,
【解析】(1)作AB的垂直平分线交AB于点M,此时点M到点A,点B和原点O这三点的距离相等.(2)利用勾股定理可求出点B的坐标,由(1)可知:M是AB的中点,从而可求出M的坐标.
【考点精析】认真审题,首先需要了解线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
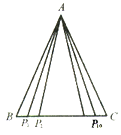
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了10次射击训练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩;
(2)求甲这10次射击成绩的方差;
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环2,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分别求出代数式a2﹣2ab+b2和(a﹣b)2的值.
①其中a=![]() ,b=3;②a=5,b=3;③a=﹣1,b=2.
,b=3;②a=5,b=3;③a=﹣1,b=2.
(2)观察(1)中的①②③你发现这两个多项式有什么关系,直接写出.
(3)利用你发现的规律,求出1.4372﹣2×1.437×0.437+0.4372的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
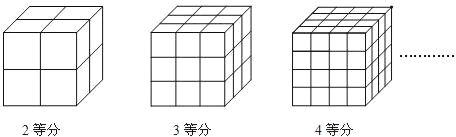
【题目】将一个正方体的表面全涂上颜色.
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
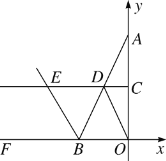
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,C,D分别是OA,AB的中点,△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________;
+1,则b=________;
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空:
已知:如图,AB∥CD,∠B=120°,CA平分∠BCD.求证:∠1=30°.
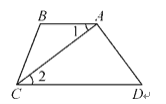
证明:∵AB∥CD( ),
∴∠B+∠BCD= ( ).
∵∠B= ( ),
∴∠BCD= ( ).
又∵CA平分∠BCD( ),
∴∠2= ( ).
∵AB∥CD( ),
∴∠1= =30°( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com