
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;

(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
【答案】(1)y=![]() x2-
x2-![]() x-1; (2)(-1,0);(3)见图象
x-1; (2)(-1,0);(3)见图象
【解析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;
(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;
(3)画出图象,再根据图象直接得出答案.
解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点,
∴ ,
,
∴a=![]() ,b=-
,b=-![]() ,c=-1,
,c=-1,
∴二次函数的解析式为y=![]() x2-
x2-![]() x-1;
x-1;
(2)当y=0时,得![]() x2-
x2-![]() x-1=0;
x-1=0;
解得x1=2,x2=-1,
∴点D坐标为(-1,0);
(3)图象如图,
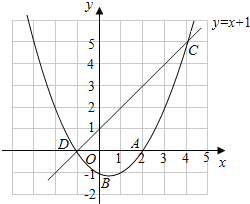
当一次函数的值大于二次函数的值时,x的取值范围是-1<x<4.
“点睛”本题考查了用待定系数法求二次函数的解析式以及一次函数的图象、抛物线与x轴的交点问题,是中档题,要熟练掌握.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式
(x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
……
(1)根据以上规律,则(x﹣1)(x6+x5+x4+x3+x2+x+1)= .
(2)你能否由此归纳出一般性规律:(x﹣1)(xn+xn﹣1+…+x+1)= .
(3)根据以上规律求1+3+32+…+334+335的结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红各自随机选择本周日的上午或下午去扬州科技馆参观.
(1) 小明、小刚本周日的上午去参观的概率为_____;
(2) 求他们三人在同一半天去参观的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个图形上所有点的纵坐标不变,横坐标乘以-1,则所得图形与原图形的关系为( )
A. 关于x轴成轴对称图形 B. 关于y轴成轴对称图形
C. 关于原点成中心对称图形 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com