
【题目】已知,正方形![]() 中,点
中,点![]() 是边
是边![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.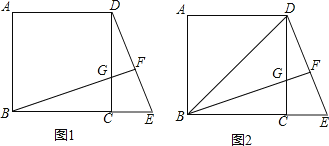
(1)如图甲,求证:![]() ;
;
(2)如图乙,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由正方形的性质得出BC=DC,∠BCG=∠DCE=90°,利用角边角证明△BGC≌△DEC,然后可得出CG=CE;
(2)由线段的和差,正方形的性质求出正方形的边长为3![]() ,根据勾股定理求出线段BD=6,过点G作GH⊥DB,根据勾股定理可得出HG=DH=2,进而求出BH=4,BG=2
,根据勾股定理求出线段BD=6,过点G作GH⊥DB,根据勾股定理可得出HG=DH=2,进而求出BH=4,BG=2![]() ,在Rt△HBG中可求出cos∠DBG的值.
,在Rt△HBG中可求出cos∠DBG的值.
解:(1)∵四边形ABCD是正方形,
∴BC=DC,∠BCG=∠DCE=90°,
又∵BF⊥DE,
∴∠GFD=90°,
又∵∠GBC+∠BGC+∠GCB=180°,
∠GFD+∠FDG+∠DGF=180°,
∠BGC=∠DGF,∴∠CBG=∠CDE,
在△BGC和△DEC中,
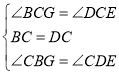 ,
,
∴△BGC≌△DEC(ASA),
∴CG=CE;
(2)过点G作GH⊥BD,设CE=x,
∵CG=CE,∴CG=x,
又∵BE=BC+CE,DC=DG+GC,BC=DC,
BE=4![]() ,DG=2
,DG=2![]() ,
,
∴4![]() x=2
x=2![]() +x,解得:x=
+x,解得:x=![]() ,∴BC=3
,∴BC=3![]() ,
,
在Rt△BCD中,由勾股定理得:
![]() ,
,
又易得△DHG为等腰直角三角形,∴根据勾股定理可得HD=HG=2,
又∵BD=BH+HD,
∴BH=6-2=4,
在Rt△HBG中,由勾股定理得:
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
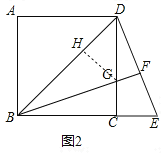
【题目】如图,二次函数![]() (其中
(其中![]() )的图像与
)的图像与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() (点
(点![]() 位于
位于![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点作
点作![]() 轴的平行线
轴的平行线![]() 交二次函数图于点
交二次函数图于点![]() .
.

(1)当![]() 时,求
时,求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过点![]() 作射线
作射线![]() 交二次函数的图像与点
交二次函数的图像与点![]() ,使得
,使得![]() ,求
,求![]() 点的坐标(用含
点的坐标(用含![]() 的式子表示)
的式子表示)
(3)在第![]() 问的条件下,二次函数
问的条件下,二次函数![]() 的顶点为
的顶点为![]() ,过点
,过点![]() 、
、![]() 作直线与
作直线与![]() 轴于点
轴于点![]() ,试求出以
,试求出以![]() 、
、![]() 、
、![]() 的长度为三边长的三角形的面积(用含
的长度为三边长的三角形的面积(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____(填序号).
①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c;
②“若ac>bc,则a>b”的逆命题是真命题;
③若点M(a,2)与N(1,b)关于x轴对称,则a+b=﹣1;
④![]() 的整数部分是a,小数部分是b,则ab=3
的整数部分是a,小数部分是b,则ab=3![]() ﹣3.
﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
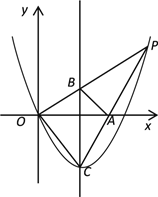
【题目】如图,已知抛物线y=ax2+bx的顶点为C(1,![]() ),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被哦感染.
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
(3)![]() 轮(
轮(![]() 为正整数)感染后,被感染的电脑有________台.
为正整数)感染后,被感染的电脑有________台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中ac≠0,a≠c.下列四个结论中:正确的个数有( )
①如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根;
②如果ac<0,方程M、N都有两个不相等的实数根;
③如果2是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
④如果方程M和方程N有一个相同的根,那么这个根必是x=1.
A.4个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com