
 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$. 分析 首先由勾股定理求出BC和CD,再利用三角形相似就可以求出结论,由条件把AM、AN用含x的式子表示出来,由勾股定理把MN表示出来解答即可.
解答 解:∵∠BAC=90°,
∴∠B+∠C=90°,
∵AD是BC边上的高,
∴∠DAC+∠C=90°
∴∠B+∠DAC=90°,
∴∠BDM+∠MDA=∠ADN+∠MDA=90°
∴∠BDM=∠ADN,
∴△BMD∽△AND,
∴$\frac{DM}{DN}=\frac{BD}{AD}$,
∵$\frac{DB}{AD}=cotB=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}$,
∴DM:DN=$\frac{3}{4}$,
∵△BMD∽△AND,
∴$\frac{BM}{AN}=\frac{BD}{AD}=\frac{3}{4}$∴,
∴AN=$\frac{4}{3}$BM∴,
设BM为x,
∴AN=$\frac{4}{3}x$,AM=6-x,
∵∠BAC=90°,
∴MN2=(6-x)2+($\frac{4}{3}$x)2=($\frac{5}{3}x-\frac{18}{5}$)2+$\frac{576}{25}$,
故MN的最小值是$\sqrt{\frac{576}{25}}=\frac{24}{5}$,
故答案为:$\frac{24}{5}$.
点评 此题考查相似三角形的性质,关键是利用勾股定理得出BC和CD,再将AM、AN用含x的式子表示出来,利用二次函数的最值计算即可.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
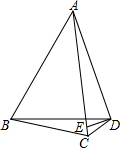 如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.
如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B向点B运动,设运动时间为t秒(t>0),
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B向点B运动,设运动时间为t秒(t>0),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运输量单价[元/(吨•千米)] | 冷藏费单价[元/(吨•时)] | 过路过桥费(元) |
| 2 | 5 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
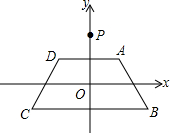 如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )
如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,-1),C(-2,-1),D(-1,1).y轴上一点P(0,2)绕点A旋转180°得点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,…,则点P2014的坐标是( )| A. | (2014,2) | B. | (2014,-2) | C. | (2012,-2) | D. | (2012,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com