
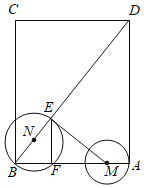
【题目】如图,在矩形ABCD中,AB=3,BC=4,半径为1的动圆圆心M从A点出发,沿着AB方向以1个单位长度/每秒的速度匀速运动,同时动点N从点B出发,沿着BD方向也以1个单位长度/每秒的速度匀速运动,设运动的时间为t秒(0≤t≤2.5),以点N为圆心,NB的长为半径的⊙N与BD,AB的交点分别为E,F,连结EF,ME.
(1)①当t= 秒时,⊙N恰好经过点M;②在运动过程中,当⊙M与△ABD的边相切时,t= 秒;
(2)当⊙M经过点B时,①求N到AD的距离;②求⊙N被AD截得的弦长;
(3)若⊙N与线段ME只有一个公共点时,直接写出t的取值范围.
【答案】(1)①![]() ,②1或
,②1或![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)0<t≤
;(3)0<t≤![]() 或
或![]() <t≤
<t≤![]()
【解析】
(1)①⊙N恰好经过点M即NM=NF=BN,过点N作NG⊥AB于G,连接NF,利用等腰三角形性质即可求得;②⊙M与△ABD的边相切可以有两种情况:⊙M与AD相切或⊙M与BD相切,利用切线性质和相似三角形性质可得结论;
(2)①过点N作NP⊥AD于点P,利用相似三角形性质即可;②由垂径定理可得:GH=2GP,利用勾股定理可求得GP;
(3)⊙N与线段EM只有一个公共点,可以有两种情况:①点M在⊙N的外部,②点M在⊙N的内部.
(1)①如图1,过点N作NG⊥AB于G,连接NF,AM=t,BM=3﹣t,

∵⊙N恰好经过点M
∴点F与M重合,即:BF=BM=3﹣t,
∵NB=NF=t,
∴BG=![]() =
=![]() (3﹣t)
(3﹣t)
∵矩形ABCD
∴∠BAD=90° AD=BC=4
∴BD=![]() =
=![]() =5
=5
∵NG⊥AB
∴∠BGN=90°=∠BAD
∴NG∥AD
∴△BNG∽△BDA
∴![]() =
=![]() =
=![]() ,即5×
,即5×![]() (3﹣t)=3t,解得:t=
(3﹣t)=3t,解得:t=![]()
故答案为:![]()
②当⊙M与AD相切时,AM=1,∴t=1
当⊙M与BD相切时,EM⊥BD,且ME=1,∵![]() =
=![]() =
=![]()
∴4(3﹣t)=5,解得t=![]()
故答案为:1或![]() ;
;
(2)①过点N作NP⊥AD于点P,当⊙M经过点B时,AM=AB﹣MB=2
∴t=2
∴BN=2,DN=BD﹣BN=3
∵NP∥AB
∴△NDP∽△BDA
∴![]() =
=![]()
∴NP=![]()
②设⊙N与AD交于G,H,连接NG,则NG=NB=2,
在Rt△GNP中,由勾股定理可得:GP=![]() =
=![]()
∴GH=2GP=![]()
(3)当点M在⊙N的外部时,线段EM与⊙N只有1个公共点,则∠BEM≥90°,
若∠BEM=90°,则![]() =
=![]() =
=![]() ,即5BE=3BM
,即5BE=3BM
∴5×2t=3(3﹣t),解得:t=![]()
∴0<t≤![]()
当点M在⊙N的内部时,线段EM与⊙N也只有1个公共点,由①知,点F与点M重合时,t=![]() ,
,
∴![]() <t≤
<t≤![]()
故t的取值范围为:0<t≤![]() 或
或![]() <t≤
<t≤![]() .
.



科目:初中数学 来源: 题型:
【题目】将108个苹果放到一些盒子中,盒子有三种规格:一种可以装10个苹果,一种可以装9个苹果,一种可以装6个苹果,要求每种规格都要有且每个盒子均恰好装满,则不同的装法总数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
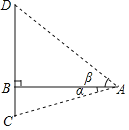
A.asinα+asinβB.acosα+acosβC.atanα+atanβD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
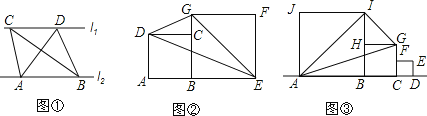
【题目】探究:如图①,直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,记△ABC的面积为S1,△ABD的面积为S2,求证:S1=S2.
拓展:如图②,E为线段AB延长线上一点,BE>AB,正方形ABCD、正方形BEFG均在直线AB同侧,求证:△DEG的面积是正方形BEFG面积的一半.
应用:如图③,在一条直线上依次有点A、B、C、D,正方形ABIJ、正方形BCGH、正方形CDEF均在直线AB同侧,且点F、H分别是边CG、BI的中点,若正方形CDEF的面积为l,则△AGI的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);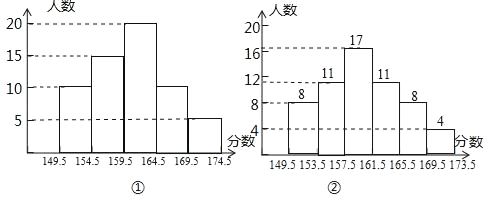
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
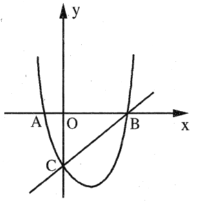
【题目】如图,二次函数的图象交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() 是直线
是直线![]() 下方抛物线上一动点.
下方抛物线上一动点.
(1)求这个二次函数的表达式;
(2)连接![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 面积最大,若存在,求出点
面积最大,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)在平面直角坐标系中,对于函数图象的横宽、纵高给出如下定义:当自变量x在![]() 范围内时,函数值y满足
范围内时,函数值y满足![]() .那么我们称b-a为这段函数图象的横宽,称d-c为这段函数图象的纵高.纵高与横宽的比值记为k即:
.那么我们称b-a为这段函数图象的横宽,称d-c为这段函数图象的纵高.纵高与横宽的比值记为k即:![]() .
.
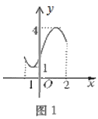
(示例)如图1,当![]() 时;函数值y满足
时;函数值y满足![]() ,那么该段函数图象的横宽为2-(-1)=3,纵高为4-1=3.则
,那么该段函数图象的横宽为2-(-1)=3,纵高为4-1=3.则![]() .
.
(应用)(1)当![]() 时,函数
时,函数![]() 的图象横宽为 ,纵高为 ;
的图象横宽为 ,纵高为 ;
(2)已知反比例函数![]() ,当点M(3,4)和点N在该函数图象上,且MN段函数图象的纵高为2时,求k的值.
,当点M(3,4)和点N在该函数图象上,且MN段函数图象的纵高为2时,求k的值.
(3)已知二次函数![]() 的图象与x轴交于A点,B点.
的图象与x轴交于A点,B点.
①若m=1,是否存在这样的抛物线段,当![]() (
(![]() )时,函数值满足
)时,函数值满足![]() 若存在,请求出这段函数图象的k值;若不存在,请说明理由.
若存在,请求出这段函数图象的k值;若不存在,请说明理由.
②如图2,若点P在直线y=x上运动,以点P为圆心,![]() 为半径作圆,当AB段函数图象的k=1时,抛物线顶点恰好落在
为半径作圆,当AB段函数图象的k=1时,抛物线顶点恰好落在![]() 上,请直接写出此时点P的坐标.
上,请直接写出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
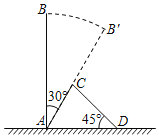
【题目】如图,某次台风来袭时,垂直于地面的大树AB被刮倾斜30°后,折断倒在地上,树的顶部恰好落在地面上点D处,大树被折断部分和地面所成的角∠ADC=45°,AD=4米,求这棵大树AB原来的高度是多少米?(结果精确到个位,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(x﹣3)(x﹣5)=m(m>0)有两个实数根α,β(α<β),则下列选项正确的是( )
A. 3<α<β<5 B. 3<α<5<β C. α<2<β<5 D. α<3且β>5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com