
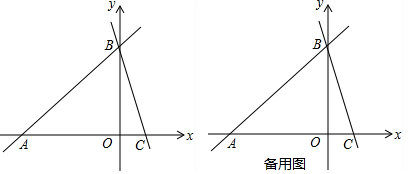
���� ��1����ȷ����A��B���꣬�����ó�n=2m�����ù��ɶ����ó�AB=$\frac{10}{3}$m��AC=2+$\frac{8}{3}$m�����жϳ�AC=AB������������⼴�ɣ�
��2�����жϳ�PQ��Сʱ��λ�ã��������������ε����ʽ������̼��ɣ�
��3�����жϳ���BFM�ա�EFM �õ���BMF=��EMF�������жϳ�����BMF�ס�OPM��BF=$\frac{9}{t}$������á�BQF�ס�AQP����������⼴�ɣ�
��� �⣺��1����ֱ��y=$\frac{3}{4}$x+2m��m��0����x�ύ�ڵ�A����y�ύ�ڵ�B��
��A��-$\frac{8}{3}$m��0����B��0��2m����
��ֱ��y=-mx+n������B��
��n=2m��
��C��2��0����
��AB=$\sqrt{��-\frac{8}{3}m��^{2}+��2m��^{2}}$=$\frac{10}{3}$m��AC=2+$\frac{8}{3}$m
�ߡ�BAO=2��OBC��
���ABO=��90��-��BAO=90��-2��OBC��
���ABC=��ABO+��OBC=90��-��OBC��
�ߡ�ACB=90��-��OBC��
��AC=AB��
��2+$\frac{8}{3}$m=$\frac{10}{3}$m��
��m=2��
��2����PQ��OAʱ��PQ������С��
��OB��OA��
��PQ��OB
���APQ�ס�ABO��
��$\frac{AQ}{AB}=\frac{AP}{AO}$=$\frac{PQ}{OB}$��
��$\frac{\frac{5}{4}t}{10}=\frac{8-t}{8}$=$\frac{PQ}{6}$��
��t=4��
��PQ=3��
��PQ����СֵΪ3��
��3����ͼ��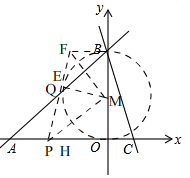
��ֱ��PQ���M�����ڵ�E����B��BF��BO��ֱ��PQ��F ����EM��FM��PM ��BM=EM��BF=EF�֡�FM=FM��
���BFM�ա�EFM
���BMF=��EMF
ͬ������PMO=��PME
�ߡ�BMF+��EMF+��PMO+��PME=180��
���BMF+��PMO=90��
�ߡ�OPM+��PMO=90�㣬
���BMF=��OPM
�֡ߡ�MBF=��POM=90�㣬
���BMF�ס�OPM
��$\frac{BF}{OM}=\frac{BM}{OP}$
��BF=$\frac{BM}{OP}��OM$=$\frac{3}{t}��3$=$\frac{9}{t}$
�ߡ�BQF�ס�AQP��
��$\frac{BF}{AP}=\frac{BQ}{AQ}$
��$\frac{\frac{9}{t}}{8-t}=\frac{10-\frac{5}{4}t}{\frac{5}{4}t}$
�ࣨ8-t��2=9
���t1=5��t2=11����ȥ��
�����ijһʱ��t��ʹֱ��PQ���M���У���ʱt=5
���� ������Բ���ۺ��⣬��Ҫ�����˵��������ε����ʣ����������ε����ʺ��ж���ȫ�������ε����ʺ��ж����Ȿ��Ĺؼ������������ߣ�Ҳ�ǽⱾ����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
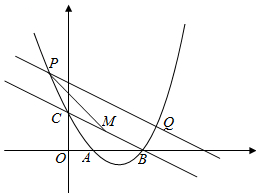 ������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2��x�ύ��A��B���㣬��y�ύ��C����PΪ��������һ���㣬����P��PQƽ��BC����������Q��P��Q��������Ϊm
������y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2��x�ύ��A��B���㣬��y�ύ��C����PΪ��������һ���㣬����P��PQƽ��BC����������Q��P��Q��������Ϊm�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
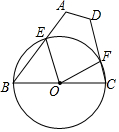 ��ͼ���ı���ABCD����AB��CD����BCΪֱ����ԲO�ֱ��ڵ�E��F������A=135�㣬��D=��120�㣬BC=4��������BOE������COF�����֮��Ϊ$\frac{5��}{3}$��
��ͼ���ı���ABCD����AB��CD����BCΪֱ����ԲO�ֱ��ڵ�E��F������A=135�㣬��D=��120�㣬BC=4��������BOE������COF�����֮��Ϊ$\frac{5��}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
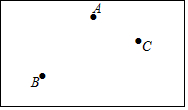 ��ͼ��С������ǰ��һ����οյأ��ڿյ��ϵĵ�A��B��C��������������С�����ھ��εĿյ��Ͻ�һ��Բ�λ�̳��ʹ�����������ڻ�̳�ı��ϣ�
��ͼ��С������ǰ��һ����οյأ��ڿյ��ϵĵ�A��B��C��������������С�����ھ��εĿյ��Ͻ�һ��Բ�λ�̳��ʹ�����������ڻ�̳�ı��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com