
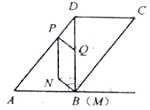
ЁОЬтФПЁПШчЭМЃЌBDЪЧЁѕABCDЕФЖдНЧЯпЃЌABЁЭBDЃЌBD=8cmЃЌAD=10cmЃЌЖЏЕуPДгЕуDГіЗЂЃЌвд5cm/sЕФЫйЖШбиDAдЫЖЏЕНжеЕуAЃЌЭЌЪБЖЏЕуQДгЕуBГіЗЂЃЌбиелЯпBDЁЊDCдЫЖЏЕНжеЕуCЃЌдкBDЁЂDCЩЯЗжБ№вд8cm/sЁЂ6cm/sЕФЫйЖШдЫЖЏ.Й§ЕуQзїQMЁЭABЃЌНЛЩфЯпABгкЕуMЃЌСЌНгPQЃЌвдPQгыQMЮЊБпзїЁѕPQMN.ЩшЕуPЕФдЫЖЏЪБМфЮЊt(s)ЃЈt>0ЃЉЃЌЁѕPQMNгыЁѕABCDжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЈcm2ЃЉ.
ЃЈ1ЃЉAP=_______cmЃЈЭЌКЌtЕФДњЪ§ЪНБэЪОЃЉ.
ЃЈ2ЃЉЕБЕуNТфдкБпABЩЯЪБЃЌЧѓtЕФжЕ.
ЃЈ3ЃЉЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЃЈ4ЃЉСЌНсNQЃЌЕБNQгыЁїABDЕФвЛБпЦНааЪБЃЌжБНгаДГіtЕФжЕ.
ЁОД№АИЁПЃЈ10-5tЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉжБНгЕУГіНсТлМДПЩЃЛ
ЃЈ2ЃЉЕБЕуNТфдкБпABЩЯЪБЃЌЫФБпаЮPNBQЮЊОиаЮЃЌЕУЕНЁїAPNЁзЁїADBЃЌгЩЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§НтД№МДПЩЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіЬжТлЃКЂйЕБPNдкЦНааЫФБпаЮФкВПЪБЃЌШчЭМ2ЃЌДЫЪБ![]() ЃЌЂкЕБNдкABЯТЗНЃЌQдкBDЩЯЪБЃЌДЫЪБ
ЃЌЂкЕБNдкABЯТЗНЃЌQдкBDЩЯЪБЃЌДЫЪБ![]() ЃЛЂлЕБNдкABЯТЗНЃЌQдкDCDЩЯЪБЃЌДЫЪБ
ЃЛЂлЕБNдкABЯТЗНЃЌQдкDCDЩЯЪБЃЌДЫЪБ![]() ЃЎ
ЃЎ
ЃЈ4ЃЉЗжШ§жжЧщПіЬжТлЃЎЂйЕБNQЁЮABЪБЃЌЂкЕБADЁЮNQЃЌЧвQдкBDЩЯЪБЃЌЂлЕБADЁЮNQЃЌЧвQдкDCЩЯЪБЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЃЈ10-5tЃЉЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌЕБЕуNТфдкБпABЩЯЪБЃЌЫФБпаЮPNBQЮЊОиаЮЃЎЁпPNЁЮDBЃЌЁрЁїAPNЁзЁїADBЃЌЁрAPЃКAD=PNЃКDBЃЌЁрЃЈ10Ѓ5tЃЉЃК10=8tЃК8ЃЌ120t=80ЃЌЁр![]() ЃЎ
ЃЎ

ЃЈ3ЃЉЗжШ§жжЧщПіЬжТлЃК
a)ШчЭМЂкЃЌЙ§ЕуPзїPEЁЭBDгкЕуEЃЌдђPE=3tЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
b)ШчЭМЂлЃЌЙ§ЕуPзїPEЁЭBDгкЕуEЃЌдђPE=3tЃЌЩшPNНЛABгкЕуFЃЌдђ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЎ
ЃЎ
c)ШчЭМЂмЃЌЕБ![]() ЪБЃЌPF=8-4tЃЌFB=3tЃЌPN=DB=QM=8ЃЌЁрFN=4tЃЌDQ=6(t-1)ЃЌЁрBM=DQ=6(t-1)ЃЎЁпЁЯGBM=ЁЯAЃЌЁЯDBA=ЁЯGMBЃЌЁрЁїBGMЁзЁїABDЃЌЁрGMЃКBM=DBЃКABЃЌНтЕУЃКGM=8t-8ЃЌЁрS=SЦНааЫФБпаЮPNMQ-SЁїFMN-SЁїBMG=8ЃЈ9t-6ЃЉЃ
ЪБЃЌPF=8-4tЃЌFB=3tЃЌPN=DB=QM=8ЃЌЁрFN=4tЃЌDQ=6(t-1)ЃЌЁрBM=DQ=6(t-1)ЃЎЁпЁЯGBM=ЁЯAЃЌЁЯDBA=ЁЯGMBЃЌЁрЁїBGMЁзЁїABDЃЌЁрGMЃКBM=DBЃКABЃЌНтЕУЃКGM=8t-8ЃЌЁрS=SЦНааЫФБпаЮPNMQ-SЁїFMN-SЁїBMG=8ЃЈ9t-6ЃЉЃ![]() ЁС4tЁСЃЈ9t-6ЃЉЃ
ЁС4tЁСЃЈ9t-6ЃЉЃ![]() ЁСЃЈ6t-6ЃЉЃЈ8t-8ЃЉ=
ЁСЃЈ6t-6ЃЉЃЈ8t-8ЃЉ=![]() ЃЎ
ЃЎ

злЩЯЫљЪіЃК 
ЃЈ4ЃЉЗжШ§жжЧщПіЬжТлЃЎ
ЂйЕБNQЁЮABЪБЃЌШчЭМ5ЃЌЙ§PзїPFЁЭBDгкFЃЌдђPF=3tЃЌDF=4tЃЌPN=FQ=BQ=8tЃЌЁрBD=8t+8t+4t=8ЃЌНтЕУЃК ![]() ЃЎ
ЃЎ
ЂкЕБADЁЮNQЃЌЧвQдкBDЩЯЪБЃЌШчЭМ6ЃЎЁпPNQDКЭPNBQЖМЪЧЦНааЫФБпаЮЃЌЁрPN=DQ=BQЃЌЁр8t+8t=8ЃЌНтЕУЃК ![]() ЃЎ
ЃЎ
ЂлЕБADЁЮNQЃЌЧвQдкDCЩЯЪБЃЌШчЭМ7ЃЌПЩвджЄУїЕБQгыCжиКЯЃЌМДжБЯпNQгыжБЯпBCжиКЯЪБЃЌТњзуЬѕМўЃЌШчЭМ8ЃЌДЫЪБDQ=AB=![]() =6ЃЌt=
=6ЃЌt=![]() =2ЃЎ
=2ЃЎ
злЩЯЫљЪіЃК ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЎ
ЃЎ






 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГаЃОХФъМЖФаЩњдкЬхФмВтЪдЕФв§ЬхЯђЩЯЯюФПЕФЧщПіЃЌЫцЛњГщШЁСЫВПЗжФаЩњв§ЬхЯђЩЯЯюФПЕФВтЪдГЩМЈЃЌЛцжЦГіШчЯТЕФЭГМЦЭМЂйКЭЭМЂкЃЎЧыИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
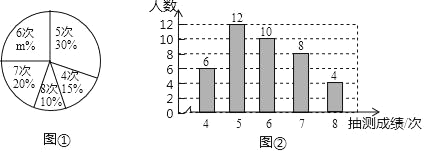
ЃЈЂёЃЉБОДЮНгЪмЫцЛњГщбљЕїВщЕФФаЩњШЫЪ§ЮЊЁЁ ЁЁЃЌЭМЂйжаmЕФжЕЮЊЁЁ ЁЁЃЛ
ЃЈЂђЃЉЧѓБОДЮЕїВщЛёШЁЕФбљБОЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂѓЃЉШєЙцЖЈв§ЬхЯђЩЯ6ДЮМАвдЩЯЃЈКЌ6ДЮЃЉЮЊИУЯюФПСМКУЃЌИљОнбљБОЪ§ОнЃЌЙРМЦИУаЃ320УћОХФъМЖФаЩњжаИУЯюФПСМКУЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() ЁЂ
ЁЂ![]() СНЕиЯрОр
СНЕиЯрОр![]() ЃЌ
ЃЌ![]() Еидк
Еидк![]() ЁЂ
ЁЂ![]() СНЕижЎМф.вЛСОНЮГЕвд
СНЕижЎМф.вЛСОНЮГЕвд![]() ЕФЫйЖШДг
ЕФЫйЖШДг![]() ЕиГіЗЂдШЫйааЪЛЃЌЧАЭљ
ЕиГіЗЂдШЫйааЪЛЃЌЧАЭљ![]() Еи.ЭЌЪБЃЌвЛСОЛѕГЕвд
Еи.ЭЌЪБЃЌвЛСОЛѕГЕвд![]() ЕФЫйЖШДг
ЕФЫйЖШДг![]() ЕиГіЗЂЃЌдШЫйааЪЛЃЌЧАЭљ
ЕиГіЗЂЃЌдШЫйааЪЛЃЌЧАЭљ![]() Еи.
Еи.
(1)ЕБСНГЕЯргіЪБЃЌЧѓНЮГЕааЪЛЕФЪБМфЃЛ
(2)ЕБСНГЕЯрОр![]() ЪБЃЌЧѓНЮГЕааЪЛЕФЪБМф.
ЪБЃЌЧѓНЮГЕааЪЛЕФЪБМф.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвде§ЗНаЮABCDвЛБпABЮЊБпзїЕШБпШ§НЧаЮABEЃЌдђЁЯCEDЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШчЭМЃЌдкЪ§жсЩЯЕуAЃЌBЫљЖдгІЕФЪ§ЪЧ-4ЃЌ4ЃЎ
![]()
ЖдгкЙигкxЕФДњЪ§ЪНNЃЌЮвУЧЙцЖЈЃКЕБгаРэЪ§xдкЪ§жсЩЯЫљЖдгІЕФЕуЮЊABжЎМф(АќРЈЕуAЃЌB)ЕФШЮвтвЛЕуЪБЃЌДњЪ§ЪНNШЁЕУЫљгажЕЕФзюДѓжЕаЁгкЕШгк4ЃЌзюаЁжЕДѓгкЕШгк-4ЃЌдђГЦДњЪ§ЪНNЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЃЎ
Р§ШчЃЌЖдгкЙигкxЕФДњЪ§ЪН|x|ЃЌЕБx=ЁР4ЪБЃЌДњЪ§ЪН|x|ШЁЕУзюДѓжЕЪЧ4ЃЛЕБx=0ЪБЃЌДњЪ§ЪН|x|ШЁЕУзюаЁжЕЪЧ0ЃЌЫљвдДњЪ§ЪН|x|ЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЃЎ
ЮЪЬтЃК
(1)ЙигкxДњЪ§ЪН|x-1|ЃЌЕБгаРэЪ§xдкЪ§жсЩЯЫљЖдгІЕФЕуЮЊABжЎМф(АќРЈЕуAЃЌB)ЕФШЮвтвЛЕуЪБЃЌШЁЕУЕФзюДѓжЕКЭзюаЁжЕЗжБ№ЪЧ____ ______ЃЎ
ЫљвдДњЪ§ЪН|x-1|__________(ЬюЪЧЛђВЛЪЧ)ЯпЖЮABЕФЗтБеДњЪ§ЪНЃЎ
(2)вдЯТЙиxЕФДњЪ§ЪНЃК
Ђй![]() ЃЛЂкx2+1ЃЛЂлx2+|x|-8ЃЛЂм|x+2|-|x-1|-1ЃЎ
ЃЛЂкx2+1ЃЛЂлx2+|x|-8ЃЛЂм|x+2|-|x-1|-1ЃЎ
ЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЪЧ__________ЃЌВЂжЄУї(жЛашвЊжЄУїЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЕФЪНзгЃЌВЛЪЧЕФВЛашжЄУї)ЃЎ
(![]() )ЙигкxЕФДњЪ§ЪН
)ЙигкxЕФДњЪ§ЪН![]() ЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЃЌдђгаРэЪ§aЕФзюДѓжЕЪЧ__________ЃЌзюаЁжЕЪЧ__________ЃЎ
ЪЧЯпЖЮABЕФЗтБеДњЪ§ЪНЃЌдђгаРэЪ§aЕФзюДѓжЕЪЧ__________ЃЌзюаЁжЕЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГПЙтЮФОпЕъЕФФГжжУЋБЪУПжЇЪлМл30дЊЃЌЪщЗЈжНУПБОЪлМл10дЊЃЎЮЊДйЯњжЦЖЈСЫСНжжгХЛнЗНАИЃКМзЗНАИЃЌТђвЛжЇУЋБЪОЭЫЭвЛБОЪщЗЈжНЃЛввЗНАИЃЌАДЙКТђЕФзмН№ЖюДђ8елЃЎФГаЃгћЮЊЪщЗЈаЁзщЙКТђетжжУЋБЪ10жЇЃЌЪщЗЈжНxЃЈxЁн10ЃЉБОЃЎ
ЃЈ1ЃЉЧѓМзЗНАИЪЕМЪИЖПюН№Жю![]() дЊгыxЕФКЏЪ§ЙиЯЕЪНКЭввЗНАИЪЕМЪИЖПюН№Жю
дЊгыxЕФКЏЪ§ЙиЯЕЪНКЭввЗНАИЪЕМЪИЖПюН№Жю![]() дЊгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
дЊгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЪдЭЈЙ§МЦЫуЮЊИУаЃЬсЙЉвЛжжНкдМЗбгУЕФЙКТђЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
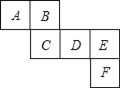
ЁОЬтФПЁПШчЭМЪЧвЛИіе§ЗНЬхЕФБэУцеЙПЊЭМЃЌЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉгыУцBЁЂCЯрЖдЕФУцЗжБ№ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєAЃНa3+a2b+3ЃЌBЃНa2bЉ3ЃЌCЃНa3Љ1ЃЌDЃНЉЃЈa2bЉ6ЃЉЃЌЧвЯрЖдСНИіУцЫљБэЪОЕФДњЪ§ЪНЕФКЭЖМЯрЕШЃЌЧѓEЁЂFЗжБ№ДњБэЕФДњЪ§ЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌвддЕу
ЃЌвддЕу![]() ЮЊЖЅЕуЕФЫФБпаЮ
ЮЊЖЅЕуЕФЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌНЋБп
ЪЧЦНааЫФБпаЮЃЌНЋБп![]() би
би![]() жсЗелЕУЕНЯпЖЮ
жсЗелЕУЕНЯпЖЮ![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() .
.
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() дк
дк![]() жсЩЯЃЌЧвЦфзјБъЮЊ
жсЩЯЃЌЧвЦфзјБъЮЊ![]() .
.
ЂйЧѓ![]() ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЫљдкжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЂкЧѓжЄЃКЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпЯрНЛгкЕу
ЕФбгГЄЯпЯрНЛгкЕу![]() ЃЌЪдЧѓ
ЃЌЪдЧѓ![]() ЕФжЕ.ЃЈжБНгаДГіД№АИЃЌВЛБиЫЕУїРэгЩЃЉ
ЕФжЕ.ЃЈжБНгаДГіД№АИЃЌВЛБиЫЕУїРэгЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
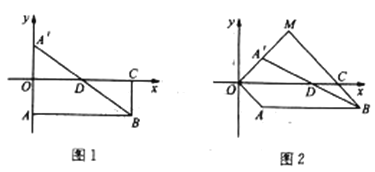
ЁОЬтФПЁПдке§ЗНаЮЭјИёжаЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕxOyЃЌЁїABCЕФШ§ИіЖЅЕуЖМдкИёЕуЩЯЃЌЕуAЕФзјБъЃЈ4ЃЌ4ЃЉЃЌЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЌВЂаДГіЕуA1ЁЂB1ЁЂC1ЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCШЦЕуCФцЪБеыа§зЊ90ЁуЃЌЛГіа§зЊКѓЕФЁїA2B2C2ЃЌВЂЧѓГіЕуAЕНA2ЕФТЗОЖГЄЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com