
【题目】一列快车从甲地始往乙地,一列慢车从乙地始往甲地,慢车的速度是快车速度的![]() ,两车同时出 发.设慢车行驶的时间为
,两车同时出 发.设慢车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系.根据图象解决以下问题:
之间的函数关系.根据图象解决以下问题:
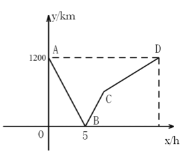
(1)甲、乙两地之间的距离为_______![]() ;点
;点![]() 的坐标为__________;
的坐标为__________;
(2)求线段![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
【答案】(1)(15,1200) (2)![]() .(3)3.7h
.(3)3.7h
【解析】
(1)根据已知条件和函数图像可以直接写出甲、乙两地之间的距离;
(2)根据题意可以求得点C的坐标,由图象可以得到点B的坐标,从而可以得到线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围.
(3)求出第一辆慢车和第二辆快车相遇时的距离,又已知快车的速度,即可用求出时间的差值.
(1)由图像可知,甲、乙两地之间的距离为1200km;
点B为两车出发5小时相遇;
∵慢车的速度和快车速度的和为:1200÷5=240km/h
又∵慢车的速度是快车速度的![]() ,
,
∴慢车的速度为:80 km/h,快车的速度为:160 km/h,
∴慢车总共行驶:1200÷80=15h
∴D(15,1200)
(2)由题可知,点C是快车刚到达乙地,
∴C点的横坐标是:1200÷160=7.5,纵坐标是1200-80×7.5=600,
即点C的坐标是(7.5,600)
设线段BC对应的函数解析式为y=kx+b,
∵点B(5,0),C(7.5,600)
∴![]() ,
,![]() ,
,
即线段BC所表示的函数关系式为:![]() .
.
(3)当第一辆慢车和第一辆快车相遇时,慢车从乙地到甲地行驶:5×80=400km,
当第一辆慢车和第二辆快车相遇时,慢车从乙地到甲地行驶:5×80+0.5×80=440km,
即此时从乙地到甲地行驶440km,
∴第二列快车比第一列快车晚出发:5.5-440÷240=3.7h


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(0,a)、B(﹣b,0),若b=![]() +4,C点是B点关于y轴的对称点.
+4,C点是B点关于y轴的对称点.
(1)判断△ABC的形状并证明;
(2)P点在第一象限,且∠APC=135°,试探究关于PA、PB、PC三条线段的确定数量关系;
(3)E点在BC上,F为线段AE的中点,EF绕E点顺时针旋转60°得到EG,E点从B点沿BC运动到C点,求G点随E点运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
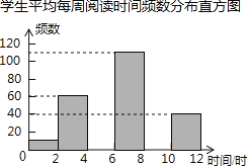
【题目】为引导学生广泛阅读古今文学名著,某校开展了读书活动.学生会随机调查了部分学生平均每周阅读时间的情况,整理并绘制了如下的统计图表:
学生平均每周阅读时间频数分布表
平均每周阅读时间x(时) | 频数 | 频率 |
0≤x<2 | 10 | 0.025 |
2≤x<4 | 60 | 0.150 |
4≤x<6 | a | 0.200 |
6≤x<8 | 110 | b |
8≤x<10 | 100 | 0.250 |
10≤x≤12 | 40 | 0.100 |
合计 | 400 | 1.000 |
请根据以上信息,解答下列问题;
(1)在频数分布表中,a=______,b=______;
(2)补全频数分布直方图;
(3)如果该校有1600名学生,请你估计该校平均每周阅读时间不少于6小时的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
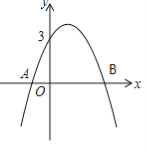
(1)求点B的坐标
(2)求该二次函数的关系式;
(3)结合图象,解答下列问题:
①当x取什么值时,该函数的图象在x轴上方?
②当-1<x<2时,求函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为准备半期考表彰的奖品,计划从友谊超市购买笔记本和水笔共40件.在获知某网店有 “双十一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费125元.
品名 商店 | 笔记本 (元/件) | 水笔 (元/件) |
友谊超市 | 5 | 2 |
网店 | 4 |
|
(1)班级购买的笔记本和水笔各多少件?
(2)求从网店购买这些奖品可节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
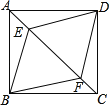
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距50千米.甲骑自行车从
两地相距50千米.甲骑自行车从![]() 地出发1.5小时后,乙骑摩托车从
地出发1.5小时后,乙骑摩托车从![]() 地出发追赶甲.已知乙的速度是甲的速度的2.5倍,且乙比甲早1小时到达
地出发追赶甲.已知乙的速度是甲的速度的2.5倍,且乙比甲早1小时到达![]() 地,求甲、乙的速度.
地,求甲、乙的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com