
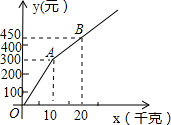
 甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.分析 (1)根据单价=总价÷数量,即可求出甲、乙两采摘园优惠前的草莓销售价格;
(2)根据数量关系结合函数图象,即可求出y1、y2与x的函数表达式;
(3)画出y1与x的函数图象,再将x=25分别代入y1、y2中求出y值,比较后即可得出结论.
解答 解:(1)300÷10=30(元/千克).
故答案为:30.
(2)根据题意得:y1=30×0.6x+50=18x+50;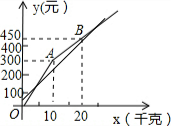
当0≤x≤10时,y2=30x;
当x>10时,y2=300+$\frac{450-300}{20-10}$(x-10)=15x+150.
∴y1=18x+50,y2=$\left\{\begin{array}{l}{30x(0≤x≤10)}\\{15x+150(x>10)}\end{array}\right.$.
(3)画出y1与x的函数图象,如图所示.
当x=25时,y1=18x+50=500,y2=15x+150=525,
∵500<525,
∴选择甲采摘园较为优惠.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据单价=总价÷数量,求出甲、乙两采摘园优惠前的草莓销售价格;(2)根据数量关系结合函数图象找出y1、y2与x的函数表达式;(3)将x=25分别代入y1、y2中求出y值.


科目:初中数学 来源: 题型:解答题
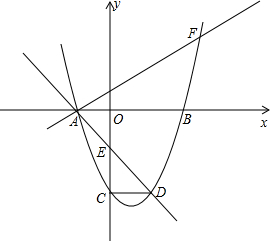 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.
如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx-5与x轴交于A、B两点(点A在点B的左侧),与y轴交点为C,直线y=-x-2经过点A,交抛物线于点D,交y轴于点E,连接CD,并且∠ADC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
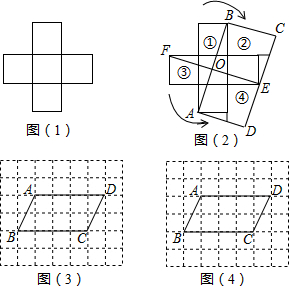
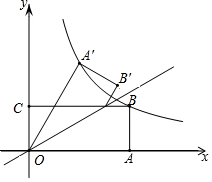 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
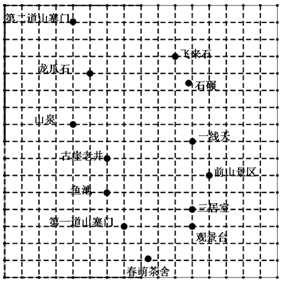 延庆区古崖居景区游览线路如图,右图是利用平面直角坐标系画出的沿途景点的大致分布示意图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示龙爪石的点的坐标为(1,3),表示古崖老井点的坐标为(2,-2),那么这个平面直角坐标系的原点所在位置是( )
延庆区古崖居景区游览线路如图,右图是利用平面直角坐标系画出的沿途景点的大致分布示意图,这个坐标系分别以正东、正北方向为x轴、y轴的正方向,如果表示龙爪石的点的坐标为(1,3),表示古崖老井点的坐标为(2,-2),那么这个平面直角坐标系的原点所在位置是( )| A. | 山泉 | B. | 鱼池 | C. | 飞来石 | D. | 石碾 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com