
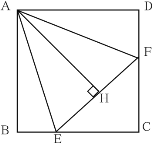
【题目】已知:正方形![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
【答案】见解析.
【解析】
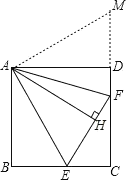
延长CD到M,使DM=BE,连接AM,证△ABE≌△ADM,推出∠DAM=∠BAE,AE=AM,求出∠FAM=∠EAF,证△EAF≌△MAF,推出EF=MF,S△EAF=S△MAF,根据三角形面积公式求出即可.
证明:延长CD到M,使DM=BE,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADF=∠ADM=∠BAD=90°,
∵∠EAF=45°,
∴∠BAE+∠DAF=45°,
在△ABE和△ADM中,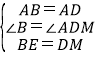 ,
,
∴△ABE≌△ADM,
∴∠DAM=∠BAE,AE=AM,
∴∠FAM=∠DAF+∠DAM=∠DAF+∠BAE=45°=∠EAF,
在△EAF和△MAF中,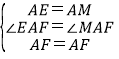 ,
,
∴△EAF≌△MAF,
∴EF=MF,S△EAF=S△MAF,
∴![]() EF×AH=
EF×AH=![]() MF×AD,
MF×AD,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]()
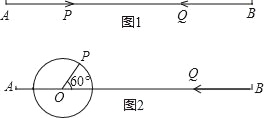
(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆![]() 的高度.先在教学楼的底端
的高度.先在教学楼的底端![]() 点处,观测到旗杆顶端
点处,观测到旗杆顶端![]() 得
得![]() ,然后爬到教学楼上的
,然后爬到教学楼上的![]() 处,观测到旗杆底端
处,观测到旗杆底端![]() 的俯角是
的俯角是![]() .已知教学楼中
.已知教学楼中![]() 、
、![]() 两处高度为
两处高度为![]() 米.
米.
(1)求教学楼与旗杆的水平距离![]() ;(结果保留根号);
;(结果保留根号);
(2)求旗杆![]() 的高度.
的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生会倡导的“爱心捐款”活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为![]() ,又知此次调查中捐15元和20元的人数共26人.
,又知此次调查中捐15元和20元的人数共26人.
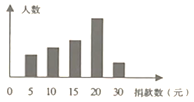
(1)他们一共抽查了______人;
(2)抽查的这些学生,总共捐款______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
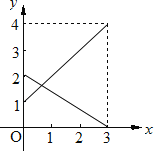
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com