
分析 先判断出点P在第三象限,再根据第三象限内点的横坐标与纵坐标都是负数列不等式组求解即可.
解答 解:∵点P(-m,1-2m)关于原点对称的点在第一象限,
∴点P在第三象限,
∴$\left\{\begin{array}{l}{-m<0①}\\{1-2m<0②}\end{array}\right.$,
解不等式①得,m>0,
解不等式②得,m>$\frac{1}{2}$,
所以,不等式组的解集是m>$\frac{1}{2}$,
即m的取值范围是m>$\frac{1}{2}$.
故答案为:m>$\frac{1}{2}$.
点评 本题考查了关于原点对称的点的坐标,解一元一次不等式组,两点关于原点对称,则两点的横、纵坐标都是互为相反数.


科目:初中数学 来源: 题型:填空题
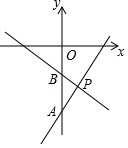 如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.
如图,一次函数y1=ax-9(a≠0)与y2=bx-3(b≠0)的图象交于点P,与y轴分别交于点A,B,若S△ABP=12,则关于x的不等式bx+6>ax的解集是x<4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时刻 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 |
| 水位高度(米) | 5 | 5.3 | 5.6 | 5.9 | 6.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
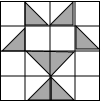 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com