
【题目】把一副扑克牌中的三张黑桃牌(它们的正面数字分别为3、4、5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你分析游戏规则对双方是否公平,并说明理由.
【答案】解:该游戏不公平,理由为:
列表如下:
3 | 4 | 5 | |
3 | (3,3) | (4,3) | (5,3) |
4 | (3,4) | (4,4) | (5,4) |
5 | (3,5) | (4,5) | (5,5) |
两人各抽取一张牌,总共有9种情况,分别为:(3,3);(3,4);(3,5);(4,3);(4,4);(4,5);(5,3),(5,4),(5,5),
其中数字相同的有3种情况,分别为(3,3);(4,4);(5,5),
∴P(小王赢)= ![]() =
= ![]() ,P(小李赢)=
,P(小李赢)= ![]() =
= ![]() ,
,
∵P(小王赢)<P(小李赢),
∴游戏规则不公平.
【解析】事件分两个步骤,第一步骤3种情况,第二步骤3种情况,共9种情况,相同的结果有3种,不同的有6种,二者的概率不等,游戏规则不公平.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
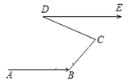
【题目】“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经 B,C,D 三点拐弯后与原来流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,则∠CDE= _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相传,大禹治水时,洛水中出现了一个“神龟”背上有美妙的图案,史称“洛书”,用现在的数字翻译出来,就是三阶幻方.三阶幻方是最简单的幻方,又叫九宫格,它是由九个数字组成的一个三行三列的矩阵.其对角线、横行、纵向的数字之和均相等,这个和叫做幻和,正中间那个数叫中心数,如图(1)是由![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所组成的一个三阶幻方,其幻和为
所组成的一个三阶幻方,其幻和为![]() ,中心数为
,中心数为![]() .如图(2)是一个新三阶幻方,该新三阶幻方的幻和为
.如图(2)是一个新三阶幻方,该新三阶幻方的幻和为![]() 的
的![]() 倍,且
倍,且![]() ,则
,则![]() _______.
_______.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为![]() 、
、![]() 、
、![]()
![]() ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为![]() ,
,![]() ,
,![]() (不计打结处丝带长度)
(不计打结处丝带长度)

(1)用含![]() 、
、![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ,
,![]() ;
;
(2)方法简介:
要比较两数![]() 与
与![]() 大小,我们可以将
大小,我们可以将![]() 与
与![]() 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:
①![]() ,则
,则![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() ,则
,则![]() ;
;
我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.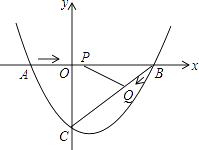
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围
的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A表示3街与5大道的十字路口,点B表示5街与3大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由A到B的一条路径,那么你能用同样的方法写出由A到B的其他几条路径吗?请至少给出3种不同的路径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: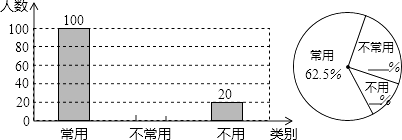
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对任意一个三位数![]() 如果
如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与![]() 的商记为
的商记为![]() .例如
.例如![]() 对调百位与十位上的数字得到
对调百位与十位上的数字得到![]() 对调百位与个位上的数字得到
对调百位与个位上的数字得到![]() 对调十位与个位上的数字得到
对调十位与个位上的数字得到![]() 这三个新三位数的和为
这三个新三位数的和为![]() 所以
所以![]() .试根据以上信息,完成下列问题:
.试根据以上信息,完成下列问题:
(1)计算:![]() __,
__,![]() __,你从中发现什么规律?你发现规律是:__.
__,你从中发现什么规律?你发现规律是:__.
(2)若![]() 都是“相异数”,
都是“相异数”,![]()
![]() ,其中x是正整数),是否存在
,其中x是正整数),是否存在![]() 满足
满足![]() ,若存在,请求出这个
,若存在,请求出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com