
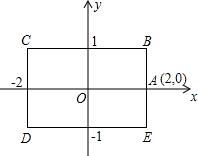
 (2012•济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
(2012•济南)如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
 (2012•济南)如图,已知双曲线y=
(2012•济南)如图,已知双曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com