
 已知:∠MON=40°,OE平分∠MON.
已知:∠MON=40°,OE平分∠MON.分析 (1)直接根据角平分线的性质即可得出结论;
(2)分AB=AD,AB=BD及AD=BD三种情况进行讨论.
解答 解:(1)∵∠MON=40°,OE平分∠MON,
∴∠MOE=$\frac{1}{2}$∠MON=20°.
故答案为:20;
(2)如图,
∵∠MON=20°,AB⊥OM,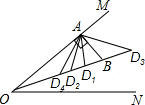
∴∠OBA=70°.
当AB=AD时,
∵∠ADB=∠OBA=70°,
∴∠DAB=20°,
∴∠OAD=90°-20°=70°;
当AB=BD时,若点D图中D2的位置时,
∵∠OBA=70°,
∴∠DAB=$\frac{180°-70°}{2}$=55°,
∴∠OAD=90°-55°=35°;
若点D图中D3的位置时,
∵∠OBA=70°,
∴∠ABD=180°-70°=110°,
∴∠BAD=$\frac{180°-110°}{2}$=35°,
∴∠OAD=90°+35°=125°;
当AD=BD时,
∵∠OAB=∠OBA=70°,
∴∠OAD=90°-70°=20°.
综上所述,∠OAD的度数为70°,35°或20°.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
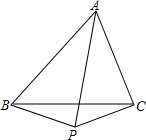 如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.
如图,在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点P,连接BP、CP.试问:∠ABP+∠ACP的度数是定值吗?请证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com