
 如图,已知点A的坐标为(0,3),矩形ABCD的面积为12,⊙P是经过A、B两点的一个动圆,当⊙P与y轴相交,且在y轴上的两交点之间的距离为4时,求圆心P的坐标.
如图,已知点A的坐标为(0,3),矩形ABCD的面积为12,⊙P是经过A、B两点的一个动圆,当⊙P与y轴相交,且在y轴上的两交点之间的距离为4时,求圆心P的坐标. 分析 先求出B点坐标,再由⊙P是经过A、B两点的一个动圆可得出圆心所在的直线方程,根据当⊙P与y轴相交,且在y轴上的两交点之间的距离为4求出另一交点的坐标,进而可得出结论.
解答 解:∵点A的坐标为(0,3),矩形ABCD的面积为12,
∴B(4,3).
∵⊙P是经过A、B两点的一个动圆,
∴圆心所在的直线方程为x=2.
∵当⊙P与y轴相交,且在y轴上的两交点之间的距离为4,
∴⊙P与y轴的另一交点坐标为(0,7)或(0,-1),
当⊙P与y轴的另一交点坐标为(0,7)时,圆心在直线y=$\frac{7+3}{2}$=5上,即P(2,5);
当⊙P与y轴的另一交点坐标为(0,-1)时,圆心在直线y=$\frac{-1+3}{2}$=1上,即P(2,1);
综上所述,P(2,5)或(2,1).
点评 本题考查的是直线与圆的位置关系,在解答此题时要注意进行分类讨论,不要漏解.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
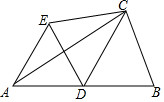 如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.
如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com