
【题目】如图,![]() ,
,![]() 均是边长为
均是边长为![]() 的等边三角形,点
的等边三角形,点![]() 是边
是边![]() 、
、![]() 的中点,直线
的中点,直线![]() 、
、![]() 相交于点
相交于点![]() .当
.当![]() 绕点
绕点![]() 旋转时,线段
旋转时,线段![]() 长的最小值是( )
长的最小值是( )

A. 2-![]() B.
B. ![]() +1 C.
+1 C. ![]() D.
D. ![]() -1
-1
【答案】D
【解析】
如图,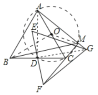
取AC的中点O,连接AD、DG、BO、OM,通过求证△DAG∽△DCF得到∠DAG=∠DCF;利用四边形的对角互补可得A、D、C、M四点共圆,继而利用三边关系可知BO≤BM+OM,即BM≥BO-OM;根据两点之间线段最短可得当M在线段BO与该圆的交点处时,线段BM最小,只需求出BO、OM的值,就可解决问题.
如图,取AC的中点O,连接AD、DG、BO、OM,∵△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,∴AD⊥BC,GD⊥EF,DA=DG,DC=DF,∴∠ADG=90°-∠CDG=∠FDC,![]() ,∴△DAG∽△DCF,∴∠DAG=∠DCF,∴A、D、C、M四点共圆,根据两点之间线段最短可得:BO≤BM+OM,即BM≥BO-OM,当M在线段BO与该圆的交点处时,线段BM最小,此时,BO=
,∴△DAG∽△DCF,∴∠DAG=∠DCF,∴A、D、C、M四点共圆,根据两点之间线段最短可得:BO≤BM+OM,即BM≥BO-OM,当M在线段BO与该圆的交点处时,线段BM最小,此时,BO=![]() =
=![]() ,OM=
,OM=![]() AC=1,则BM=BO-OM=
AC=1,则BM=BO-OM=![]() -1,故答案选D.
-1,故答案选D.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC各顶点的坐标分别为A(-3,2),B(-4,-3),C(-1,-1)

(1)画出△ABC,并画出△ABC关于y轴对称的△A1B1C1,并写出A的对应点A1的坐标.
(2)尺规作图,∠A的角平分线AD,交BC于点D(保留作图痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四 边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在X轴上,直线BD交Y轴于点F,交OE于点H,线段BC、OC的长是方程x2-6x+8=0的两个根,且OC>BC.
(1)求直线BD的解析式.
(2)求 △OFH的面积.
(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的部分图象如图所示,则下列结论中正确的是( )

A. a>0
B. 不等式ax2+bx+c>0的解集是﹣1<x<5
C. a﹣b+c>0
D. 当x>2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】期末,学校为了调查这学期学生课外阅读情况,随机抽样调查了一部分学生阅读课外书的本数,并将收集到的数据整理成如图的统计图.

(1)这次一共调查的学生人数是_______人;
(2)所调查学生读书本数的众数是_______本,中位数是_______本.
(3)若该校有800名学生,请你估计该校学生这学期读书总数是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式,例如:![]() .
.
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:像![]() ,
,![]() ,…这样的分式是假分式;像
,…这样的分式是假分式;像![]() ,
,![]() ,…这样的分式是真分式.
,…这样的分式是真分式.
类似的,假分式也可以化为整式与真分式的和(差)的形式.
例如:将分式![]() 拆分成一个整式与一个真分式的和(差)的形式.
拆分成一个整式与一个真分式的和(差)的形式.
方法一:解:由分母为![]() ,可设
,可设![]()
则由![]()
对于任意![]() ,上述等式均成立,
,上述等式均成立,
∴![]() ,解得
,解得![]()
∴![]()
这样,分式![]() 就被拆分成一个整式与一个真分式的和(差)的形式.
就被拆分成一个整式与一个真分式的和(差)的形式.
方法二:解:
![]()
这样,分式![]() 就拆分成一个整式与一个真分式的和(差)的形式.
就拆分成一个整式与一个真分式的和(差)的形式.
(1)请仿照上面的方法,选择其中一种方法将分式![]() 拆分成一个整式与一个真分式的和(差)的形式;
拆分成一个整式与一个真分式的和(差)的形式;
(2)已知整数![]() 使分式
使分式![]() 的值为整数,求出满足条件的所有整数
的值为整数,求出满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).

(1) 上述操作能验证的等式是__________________;
(2) 应用你从(1)得出的等式,完成下列各题:
①已知x24y2=12,x+2y=4,求x2y的值.
②计算:(1![]() )(1
)(1![]() )(1
)(1![]() )…(1
)…(1![]() )(1
)(1![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com