
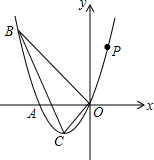
 ��ͼ����֪�����߾�����A��-2��0������B��-3��3����ԭ��O������ΪC��
��ͼ����֪�����߾�����A��-2��0������B��-3��3����ԭ��O������ΪC������ ��1�����ݴ���ϵ����������A��B��O������������������߽���ʽ��
��2����B��C����������OB��OC�ij����ҿ���á�BOC=90�㣬���P�����꣬�ɱ�ʾ��PM��AM�ij�������PMA�͡�BOC����ʱ�ɵõ�$\frac{PM}{OB}$=$\frac{AM}{OC}$��$\frac{PM}{OC}$=$\frac{AM}{OB}$���Ӷ������P�����ꣻ
��3��AOΪ�ı��ε�һ��ʱ����E��ED��AO����DE=AO=2��������D��ĺ����꣬�Ӷ������D�����꣮
��� �⣺
��1���������߽���ʽΪy=ax2+bx+c��a��0����
��A��-2��0����B��-3��3����O��0��0������ɵ�
$\left\{\begin{array}{l}{4a-2b+c=0}\\{9a-3b+c=3}\\{c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=2}\\{c=0}\end{array}\right.$��
�������߽���ʽΪy=x2+2x��
��2�����ڣ��������£�
��y=x2+2x=��x+1��2-1��
��C��������-1��-1����
���AOC=45�㣬OC=$\sqrt{2}$��
��B��-3��-3����
���BOA=45�㣬OB=3$\sqrt{2}$��
���BOC=90�㣬
��P��PM��x���ڵ�M������AP����ͼ1��
��P��������x��x2+2x����
��P���ڵ�һ���ޣ�
��PM=x2+2x��AM=AO+OM=x+2��
�ߡ�PMA=��BOC=90�㣬
�൱��PMA�͡�BOC����ʱ����$\frac{PM}{OB}$=$\frac{AM}{OC}$��$\frac{PM}{OC}$=$\frac{AM}{OB}$��
�ٵ�$\frac{PM}{OB}$=$\frac{AM}{OC}$ʱ������$\frac{{x}^{2}+2x}{3\sqrt{2}}$=$\frac{x+2}{\sqrt{2}}$����x2-x-6=0�����x=3��x=-2����ȥ����
��ʱP������Ϊ��3��15����
�ڵ�$\frac{PM}{OC}$=$\frac{AM}{OB}$ʱ������$\frac{{x}^{2}+2x}{\sqrt{2}}$=$\frac{x+2}{3\sqrt{2}}$����3x2+5x-2=0�����x=$\frac{1}{3}$��x=-2����ȥ����
��ʱP������Ϊ��$\frac{1}{3}$��$\frac{7}{9}$����
���Ͽ�֪��������������P�㣬������Ϊ��3��15����$\frac{1}{3}$��$\frac{7}{9}$����
��3�����ڣ�D������Ϊ��1��3����-3��3����
����A��O��D��EΪ�����ƽ���ı���ʱ����AOΪ�ߣ�
����DE=AO=2����DE��AO��
��D��ֻ����x���Ϸ���
����E��DE��x�ᣬ�����������D����ͼ2��
��D�������Ϊx��
��E���������߶Գ����ϣ�
��E�������Ϊ-1��
��DE=|x+1|=2��
���x=1��x=-3��
��D��������1��3����-3��3����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ�����������ߵĶ��������Գ��ᡢ���������ε��ж������ʡ�ƽ���ı��ε����ʼ���������˼��ȣ��ڣ�2������á�BOC=90���ǽ���Ĺؼ���ע�����������εĶ�Ӧ��ϵ���ڣ�3����ȷ����D���λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 19 | B�� | 25��32 | C�� | 25 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����������ABC�У�BC=5$\sqrt{2}$����ABC=45�㣬BDƽ�֡�ABC��M��N�ֱ���BD��BC�ϵĶ��㣬��CM+MN����Сֵ��5��
�����������ABC�У�BC=5$\sqrt{2}$����ABC=45�㣬BDƽ�֡�ABC��M��N�ֱ���BD��BC�ϵĶ��㣬��CM+MN����Сֵ��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
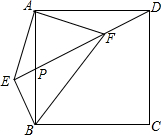 ��ͼ��������ABCD�У�PΪAB�е㣬BE��DP��DP�ӳ�����E������AE��AF��AE��DP��F������BF��CF�����н��ۣ���EF=$\sqrt{2}$AF����AB=FB����CF��BE����EF=CF��������ȷ�Ľ����У�����������
��ͼ��������ABCD�У�PΪAB�е㣬BE��DP��DP�ӳ�����E������AE��AF��AE��DP��F������BF��CF�����н��ۣ���EF=$\sqrt{2}$AF����AB=FB����CF��BE����EF=CF��������ȷ�Ľ����У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
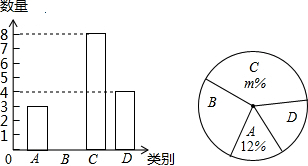
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵ�������ABCD�У�AB��DC��AB=16cm��CD=10cm��AD=5cm DE��AB������ΪE����P�ӵ�A��������2cm/����ٶ���AB���յ�B�˶�����Q�ӵ�C��������1cm/����ٶ���CD���յ�D�˶���P��Q�����У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룮
��ͼ���ڵ�������ABCD�У�AB��DC��AB=16cm��CD=10cm��AD=5cm DE��AB������ΪE����P�ӵ�A��������2cm/����ٶ���AB���յ�B�˶�����Q�ӵ�C��������1cm/����ٶ���CD���յ�D�˶���P��Q�����У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com