
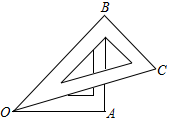
 如图,将一副三角板摆放在一起
如图,将一副三角板摆放在一起分析 (1)结合图形,计算即可;
(2)根据题意分别求出∠BOD和∠COD的度数,根据角平分线的定义计算即可.
解答 解:(1)∠AOC=45°-30°=15°,
射线OA、OB、OC组成所有小于平角的角的和为:45°+30°+15°=90°,
故答案为:15°;90°;
(2)∠BOD=180°-45°=135°,∠COD=180°-15°=165°,
∵OE为∠BOD的平分线,OF为∠COD的平分线,
∴∠DOF=$\frac{1}{2}$∠COD=82.5°,∠DOE=$\frac{1}{2}$∠DOB=67.5°,
∴∠EOF=∠DOF-∠DOE=15°.
点评 本题考查的是角的计算、角平分线的定义,掌握角平分线的定义、根据图形正确列出算式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com