
如图∠DAB=∠CAE,请补充一个条件: ,使△ABC∽△ADE.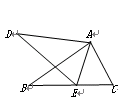
∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD•AC=AB•AE
解析试题分析:根据相似三角形的判定方法,已知一组角相等则再添加一组相等的角可该角的两个边对应成比例即可推出两三角形相似.
∵∠DAB=∠CAE
∴∠DAE=∠BAC
∴当∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD•AC=AB•AE时两三角形相似.
考点:此题考查了相似三角形的判定
点评:相似三角形的判定方法有:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源:新教材新学案 数学 八年级上册 题型:044
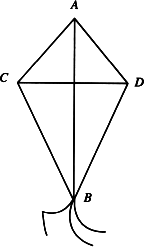
小红做了一个如图所示的风筝,其中∠CAB=∠DAB,CA=DA,小红不用测量就知道CB=DB,这是为什么?试说明理由.
查看答案和解析>>
科目:初中数学 来源:黄冈重点作业 初三数学(下) 题型:044
已知:如图所示,⊙O和⊙ 相交于A、B两点,AC是⊙
相交于A、B两点,AC是⊙ 的切线,交⊙O于点C,连结CB并延长交⊙
的切线,交⊙O于点C,连结CB并延长交⊙ 于点F,D为⊙
于点F,D为⊙ 上的点,且∠DAB=∠C,连结DB并延长交⊙O于点E.
上的点,且∠DAB=∠C,连结DB并延长交⊙O于点E.

(1)求证:DA是⊙O的切线;
(2)求证:AC2∶AD2=BC∶BD;
(3)若BF=4,CA=3 ,求DE的长
,求DE的长
查看答案和解析>>
科目:初中数学 来源:北京市四中2011-2012学年七年级下学期期中考试数学试题 题型:013
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.

A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com