
分析 (1)根据“售价比100元多20%时,销售30件可获利3000元”列方程求出a的值;
(2)列出A方案和B方案的盈利QA、QB与x的关系式,根据A方案和B方案销售月利润的最大值相同列方程求出b的值;
(3)把x=5000代入QA、QB,可作出选择.
解答 解:(1)∵售价比100元多20%,
∴售价为:120元,
则每件利润为:(120-a),
∴(120-a)×30=3000,
解得:a=20;
(2)QA=(y-20)x-62500=-$\frac{1}{100}$(x-6500)2+360000,
QB=(150-b)x-$\frac{1}{100}$x2=-$\frac{1}{100}$[x-50(150-b)]2+25(150-b)2,
∵A方案和B方案销售月利润的最大值相同,
∴360000=25(150-b)2
解得:b1=30,b2=270(舍去),
所以b=30;
(3)当x=5000时,
QA═-$\frac{1}{100}$(5000-6500)2+360000=337500,
QB=-$\frac{1}{100}$[5000-6000]2+25×1202=350000,
所以选择B方案.
点评 本题考查了二次函数在实际生活中的应用,根据利润的关系式分别写出QA、QB与x的函数关系式是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
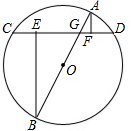 如图,AB是⊙O的直径,弦CD与AB相交于点G,过点A,B分别向弦CD作垂线,垂足分别为F、E
如图,AB是⊙O的直径,弦CD与AB相交于点G,过点A,B分别向弦CD作垂线,垂足分别为F、E查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com