
(本题14分)如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连结DF,DE, EF. 过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).
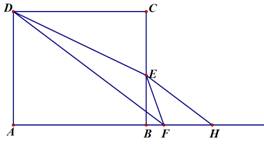
1.(1) 填空:当t= 时,AF=CE,此时BH= ;
2.(2)当△BEF与△BEH相似时,求t的值;
3.(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.
① 求S关于t的函数关系式;
② 直接写出C的最小值.
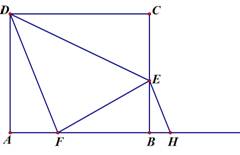
1.(1) 填空:当![]() ,(1分)AF=CE, 此时
,(1分)AF=CE, 此时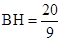 ;(2分)
;(2分)
2.(2)由EH∥DF得∠AFD=∠BHE,又∵∠A=∠CBH=90°
∴△EBH∽△DAF ∴![]() 即
即![]() ∴BH=
∴BH=![]() (2分)
(2分)
当点F在点B的左边时,即t<4时,BF=12-3t
此时,当△BEF∽△BHE时:![]() 即
即![]() 解得:
解得:![]() (1分)
(1分)
此时,当△BEF∽△BEH时: 有BF=BH, 即![]() 解得:
解得:![]() (1分)
(1分)
当点F在点B的右边时,即t>4时,BF=3t-12
此时,当△BEF∽△BHE时:![]() 即
即![]() 解得:
解得:![]() (2分)
(2分)
3.(3)① ∵EH∥DF
∴△DFE的面积=△DFH的面积=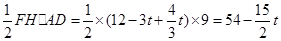 (3分)
(3分)
(其他解法若正确,酌情给分)
② 直接写出C的最小值=![]() (2分)
(2分)
解析:略


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
(本题14分)如图,已知正比例函数和反比例函数的图象都经过点![]() .
.

(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与![]() 轴、
轴、![]() 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使![]() 的面积
的面积![]() 与
与![]() 的面积S满足:
的面积S满足:![]() ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 (3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011届上海市黄浦区数学学业考试模拟试卷 题型:解答题
(本题14分)如图11,在△ABC中,∠ACB= ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,
CH⊥BM于H.
(1)试求sin∠MCH的值;
(2)求证:∠ABM=∠CAH;
(3)若D是边AB上的点,且使△AHD为等腰三角形,请直接写出AD的长为________.
查看答案和解析>>
科目:初中数学 来源:2011-2012年浙江省仙岩二中九年级数学模拟试题数学卷 题型:解答题
(本题14分)如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的长;
(2)设CP=x, △PDQ的面积为y,求y关于x的函数表达式,并求自变量的取值范围;
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省宿迁市)九年级第二次联考数学试卷(解析版) 题型:解答题
(本题14分)如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥AC,交AC的延长线于点E.

(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AE=8,⊙O的半径为5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com