
 如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH,
如图,将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH,分析 (1)首先确定A、B、C三点向右平移2格后所得对应点D、E、F三点的位置,然后再连接,然后再向上平移3格可得G、P、H三点位置,再连接即可;
(2)根据平移的性质可得AC既平行又相等的线段有DF,GH;根据平移的性质可得与∠BAC相等的角是∠D,∠G,根据平行线的性质可得与∠BAC相等的角还有∠AMD,∠CME;
(3)由平移性质得:PH∥BC,AB∥ED,根据三角形内角和计算出∠BCA的度数,再利用平行线的性质可得∠BCA=∠HAC=105°,再利用平行线的性质计算出∠B=∠MEC,再根据三角形内角和外角的关系可得∠DMC的度数.
解答 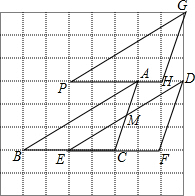 解:(1)如图所示:
解:(1)如图所示:
(2)根据平移可得与AC既平行又相等的线段是DF,GH;
根据平移可得与∠BAC相等的角是∠D,∠G,
∵AC∥DF,
∴∠D=∠AMD=∠CME;
故答案为:DF,GH;∠D,∠G,∠AMD,∠CME.
(3)由平移性质得:PH∥BC,AB∥ED,
∵∠BAC=43°,∠B=32°,
∴∠BCA=180°-(∠BAC+∠B)=180°-75°=105°,
∵PH∥BC,
∴∠BCA=∠HAC=105°,
∵AB∥ED,
∴∠B=∠MEC=32°,
∴∠DMC=∠MEC+∠BCA=32°+105°=137°.
点评 此题主要考查了作图--平移变换,以及平移的性质,关键是掌握图形是有点组成的,平移图形时,只要找出组成图形的关键点平移后的位置即可.平移后图形的形状和大小不变.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | y=-2x+40(0<x<20) | B. | y=-0.5x+20(10<x<20) | ||
| C. | y=-2x+40(10<x<20) | D. | y=-0.5x+20(0<x<20) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
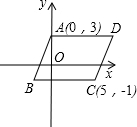 如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).
如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com