
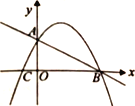
【题目】如图,直线![]() 交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
(1)求抛物线的表达式.
(2)当点M在线段AB上方的曲线上移动时,求四边形AOBM的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;
;
【解析】
(1)由直线解析式可求出A、B两点坐标,由AC⊥AB,可证明ΔAOC∽ΔBOA,根据相似三角形的性质可求出OC的长,即可得C点坐标,利用待定系数法即可得出抛物线的解析式;(2)过M点作MN⊥x轴,交直线AB于D点,设M点的横坐标为a,可得出M点和D点坐标,进而求出MD的长,可得△ABM的面积,根据S四边形AOBM=S△AOB+S△ABM可得关于a的二次函数,根据二次函数的性质即可求出四边形AOBM面积的最大值;
(1)∵直线![]() 交坐标轴A、B两点,
交坐标轴A、B两点,
∴A(0,2)、B(4,0),
∴OA=2,OB=4,
∵AC⊥AB,OA⊥BC,
∴∠AOB=∠AOC=90°,∠OAC+∠OAB=90°,∠OAC+∠OCA=90°,
∴∠OCA=∠OAB,
∴ΔAOC∽ΔBOA
∴![]() ,
,
解得:OC=1
∴C(-1,0)
设抛物线的表达式为:![]() ,得
,得 ,
,
解得 ,
,
∴抛物线的表达式为:![]()
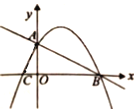
(2)过M点作MN⊥x轴,交直线AB于D点
设M点的横坐标为a,则M(a,![]() )、D(a,
)、D(a,![]() )
)
∴![]()
∴![]()
∴![]()
当a=2时,![]() 的值最大,则
的值最大,则![]()


科目:初中数学 来源: 题型:
【题目】已知方程![]() ,
,
(1)求证:方程一定有两个不相等的实数根;
(2)![]() 取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
取何值时,方程二根中一个比3大,一个比3小。(可用数形结合来解)
(3)![]() 取何值时方程的两个根异号且负的实数根的绝对值大.
取何值时方程的两个根异号且负的实数根的绝对值大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(m,3),B(-3,n)两点.
的图象交于A(m,3),B(-3,n)两点.
(1)求一次函数的解析式;
(2)观察函数图象,直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD交于点O.过点C作BD的平行线,过点D作AC的平行线,两直线相交于点E.
(1)求证:四边形OCED是矩形;
(2)若CE=1,DE=2,ABCD的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
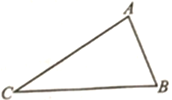
【题目】如图,△ABC中,AC=8,BC=10,AC>AB.
(1)用尺规作图法在△ABC内求作一点D,使点D到两点A、C的距离相等,又到边AC、BC的距离相等(保留作图痕迹,不写作法).
(2)若△ACD的周长为18,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加,据统计,某小区![]() 年底拥有家庭轿车
年底拥有家庭轿车![]() 辆,
辆,![]() 年底家庭轿车的拥有量达到
年底家庭轿车的拥有量达到![]() 辆.
辆.
(1)若该小区![]() 年底到
年底到![]() 年底家庭轿车拥有量的年平均增长率都相同,求该小区到
年底家庭轿车拥有量的年平均增长率都相同,求该小区到![]() 年底家庭轿车将达到多少辆?
年底家庭轿车将达到多少辆?
(2)为了解决停车困难,该小区决定投资![]() 万元再建造若干个停车位,据测算,室内车位建造费用
万元再建造若干个停车位,据测算,室内车位建造费用![]() 元
元![]() 个,露天车位建造费用
个,露天车位建造费用![]() 元
元![]() 个,考虑到实际因素,计划露天车位的数量不少于室内车位的
个,考虑到实际因素,计划露天车位的数量不少于室内车位的![]() 倍,但不超过室内车位的
倍,但不超过室内车位的![]() 倍,求该小区建造车位共有几种方案?
倍,求该小区建造车位共有几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
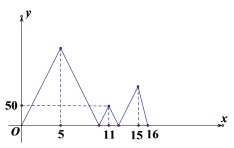
【题目】小亮和小花约定周六早晨在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,小亮以较快的速度匀速跑到点B休息1分钟后立即原速跑回A点,小花先匀速慢跑了5分钟后,把速度提高到原来的![]() 倍,又经过6分钟后超越了小亮一段距离,小花又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的小亮,然后立即以出发时的速度跑回A点.若两人之间的距离记为y(米),小花的跑步时间记为x(分),y和x的部分函数关系如图所示,则当小亮回到A点时小花距A点________米.
倍,又经过6分钟后超越了小亮一段距离,小花又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的小亮,然后立即以出发时的速度跑回A点.若两人之间的距离记为y(米),小花的跑步时间记为x(分),y和x的部分函数关系如图所示,则当小亮回到A点时小花距A点________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.
(1)甲、乙两种笔记本的进价分别是多少元?
(2)该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?
(3)店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高![]() 元,在不考虑其他因素的条件下,当
元,在不考虑其他因素的条件下,当![]() 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
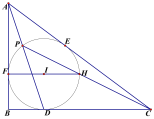
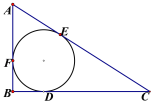
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com