
分析 求出数列的前4项,继而得出数列的循环周期,然后求解可得.
解答 解:∵a1=$\frac{1}{2}$,
a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{1-\frac{1}{2}}$=2,
a3=$\frac{1}{1-{a}_{2}}$=$\frac{1}{1-2}$=-1,
a4=$\frac{1}{1-{a}_{3}}$=$\frac{1}{1-(-1)}$=$\frac{1}{2}$,
…
∴这列数每3个数为一周期循环,
∵2017÷3=672…1,
∴a2017=a1=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查数字的变化规律,解决此类问题时通常需要确定数列与序数的关系或者数列的循环周期等,此题得出这列数每3个数为一周期循环是解题的关键.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
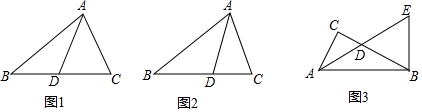
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
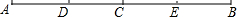 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )| A. | AC=2CE | B. | AB-AD=2CD | C. | AD=$\frac{1}{3}$DB | D. | DE=$\frac{1}{2}$AB |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com