
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
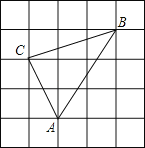
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
【答案】(1)![]() ;(2)△ABC不是直角三角形,理由见解析;(3)
;(2)△ABC不是直角三角形,理由见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据勾股定理求出△ABC的三条边长,再将三条边长相加即可得出该三角形的周长;
(2)根据勾股定理的逆定理判定即可;
(3)利用图形知S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF;
(4)设点C到AB的距离是h,则根据三角形的面积公式知![]() ABh=
ABh=![]() ,据此可以求得h的值.
,据此可以求得h的值.
(1)根据勾股定理知,BC=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ,AB=
,AB=![]() =
=![]() ,
,
故△ABC的周长=AB+BC+AC=![]()
![]() ;
;
(2)△ABC不是直角三角形,理由如下:
由(1)可知,BC=![]() ,AC=
,AC=![]() ,AB=
,AB=![]() ,AC<BC<AB,
,AC<BC<AB,
∵![]() ,
,
∴△ABC不是直角三角形;
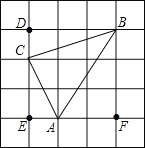
(3)如图,
S△ABC=S正方形BDEF﹣S△BCD﹣S△ACE﹣S△ABF
=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×2﹣
×1×2﹣![]() ×2×3
×2×3
=![]() ;
;
(3)设点C到AB的距离是h.
由(3)知,三角形ABC的面积是![]() ,则
,则![]() ABh=
ABh=![]() ,即
,即![]() ×
×![]() h=
h=![]() ,
,
解得,h=![]() ,即点C到AB的距离为
,即点C到AB的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
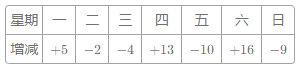
(1)产量最多的一天比产量最少的一天多生产 辆?
(2)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖20元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴,直线y=﹣x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2,那么ABCD面积为_____.
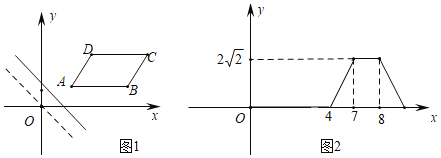
查看答案和解析>>
科目:初中数学 来源: 题型:
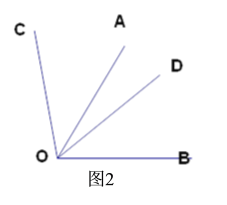
【题目】(1)如图 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代数式表示∠BOC.

(2)如图2,若∠AOB=∠COD=60°,直接写出∠AOC与∠BOD的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+bx+c(b,c都是常数)的图象经过点(1,0)和(0,2).
(1)当﹣2≤x≤2时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m+n=1,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() “明天降雨的概率是
“明天降雨的概率是![]() ”表示明天有半天都在降雨;
”表示明天有半天都在降雨;
![]() 无理数是开方开不尽的数;
无理数是开方开不尽的数;
![]() 若
若![]() 为实数,则
为实数,则![]() 是不可能事件;
是不可能事件;
![]() 的平方根是
的平方根是![]() ,用式子表示是
,用式子表示是![]() ;
;
![]() 某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com