
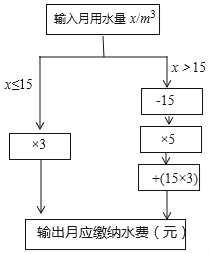
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
【答案】(1) 18,4,55;(2) 5x﹣30;(3)20
【解析】
(1)根据用水量的多少和两种不同的计算方法计算水费即可;
(2)用15立方米的水费加上比15立方米多的部分的水费即可;
(3)代入总水费150元,求得用水量即可.
(1)张大爷水费:6×3=18元;
王阿姨水费:15×3=45元;
小明家水费:(17﹣15)×5+15×3=55元.
故答案为:18,4,55.
(2)观察示意图得:当x>15时,月应缴纳水费(元)用x的代数式表示为15×3+5(x﹣15)=5x﹣30;
故答案为:5x﹣30;
(3)(70﹣15×3)÷5+15=25÷5+15=5+15=20(m3).
答:小丽家该月用水20m3.
故答案为:20;


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)试验探索:
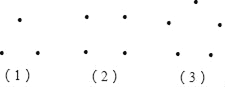
如果过每两点可以画一条直线,那么请下面三组图中分别画线,并回答问题:
第(1)组最多可以画______条直线;
第(2)组最多可以画______条直线;
第(3)组最多可以画______条直线.
(2)归纳结论:
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线______条.(作用含n的代数式表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点在坐标轴上,点A的坐标为(﹣3,0),假设有甲,乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按顺时针方向匀速运动,物体乙按逆时针方向匀速运动,若物体甲12秒钟可环绕一周回到点A,物体乙24秒钟可环绕一周回到点A,则两个物体运动后的第2017次相遇地点的坐标是 . 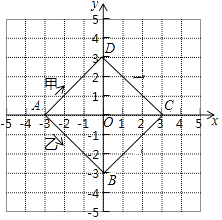
查看答案和解析>>
科目:初中数学 来源: 题型:
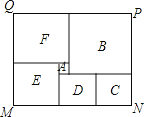
【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图。(要求每位同学只能选择一种自己喜欢的球类;扇形统计图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数)请你根据图中提供的信息,解答下列问题:
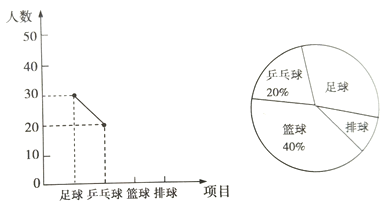
(1)在这次研究中,一共调查了多少名学生?
(2)喜欢排球的人数在扇形统计图中所对应的扇形的圆心角是多少度?
(3)补全频数分布折线统计图。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(一), ![]() 为一条拉直的细线,A、B两点在
为一条拉直的细线,A、B两点在 ![]() 上,且
上,且 ![]() :
: ![]() =1:3,
=1:3, ![]() :
: ![]() =3:5.若先固定B点,将
=3:5.若先固定B点,将 ![]() 折向
折向 ![]() ,使得
,使得 ![]() 重迭在
重迭在 ![]() 上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( ) 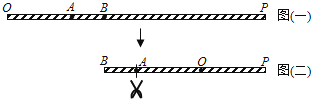
A.1:1:1
B.1:1:2
C.1:2:2
D.1:2:5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com