
 如图,AO=BO=2,∠AOB=90°,△A′、C、D分别与点A重合,在边BO上、在边BO的延长线上,且A′C=A′D=$\sqrt{5}$,将△A′CD沿射线OB平移,设平移距离为x(其中0<x<3),平移后的图形与△ABO重叠部分的面积为S.
如图,AO=BO=2,∠AOB=90°,△A′、C、D分别与点A重合,在边BO上、在边BO的延长线上,且A′C=A′D=$\sqrt{5}$,将△A′CD沿射线OB平移,设平移距离为x(其中0<x<3),平移后的图形与△ABO重叠部分的面积为S.分析 (1)勾股定理求出OD,再根据正切函数定义可得;
(2)分0<x≤1和1<x<3两种情况,当0<x≤1时,设A′C与AB相交于点P,作PQ⊥BO于点Q,设A′D与AB相交于点M,与AO相交于点N,作MR⊥AO于点R,设PQ=h,MR=h′,解直角三角形分别得出CQ=$\frac{1}{2}$h、AR=h′、RN=MRtan∠RMN=h′tan(90°-∠MNR)=h′tan(90°-∠DNO)=h′tanD=2h′,由PQ=BQtanB=BQ即h=(1-x)+$\frac{1}{2}$h,得h=2(1-x),AN=AO-ON=2-ODtanD=2-2(1-x)=2x及AR+RN=AN得h′=$\frac{2}{3}$x,最后根据S=S△ABO-S△PBC-S△AMN可得函数解析式;当1<x<3时,设A′D与AB相交于点P,作PQ⊥BO于点Q,同理得BQ=PQ即3-x=h+$\frac{1}{2}$h,得h=$\frac{2}{3}$(3-x),根据三角形面积公式可得此时函数解析式.
解答 解:(1)如图1,
∵∠AOB=90°,
∴OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{5-{2}^{2}}$=1,
∴tanD=$\frac{AO}{OD}$=$\frac{2}{1}$=2;
(2)如图1,同理,OC=1,tan∠A′CD=2,tan∠BAO=tanB=1,
当0<x≤1时,如图2,
设A′C与AB相交于点P,作PQ⊥BO于点Q,设A′D与AB相交于点M,与AO相交于点N,作MR⊥AO于点R,
设PQ=h,MR=h′,
在Rt△PCQ中,PQ=CQtan∠PCQ,得CQ=$\frac{1}{2}$h,
在Rt△PBQ中,PQ=BQtanB=BQ,即h=(1-x)+$\frac{1}{2}$h,得h=2(1-x),
在Rt△AMR中,MR=ARtan∠BAO=AR,即AR=h′,
在Rt△MNR中,RN=MRtan∠RMN=h′tan(90°-∠MNR)=h′tan(90°-∠DNO)=h′tanD=2h′,
∵AN=AO-ON=2-ODtanD=2-2(1-x)=2x,
AR+RN=AN,即h′+2h′=2x,得h′=$\frac{2}{3}$x,
∴S=S△ABO-S△PBC-S△AMN
=$\frac{1}{2}$AO×BO-$\frac{1}{2}$BC×PQ-$\frac{1}{2}$AN×MR
=$\frac{1}{2}$×2×2-$\frac{1}{2}$×(1-x)×2(1-x)-$\frac{1}{2}$×2x×$\frac{2}{3}$x
=-$\frac{5}{3}$x2+2x+1;
当1<x<3时,如图3,设A′D与AB相交于点P,作PQ⊥BO于点Q,
设PQ=h,同理得BQ=PQ,
∴3-x=h+$\frac{1}{2}$h,
得h=$\frac{2}{3}$(3-x),
∴S=$\left\{\begin{array}{l}{-\frac{5}{3}{x}^{2}+2x+1}&{(0<x≤1)}\\{\frac{1}{3}{x}^{2}-2x+3}&{(1<x<3)}\end{array}\right.$.
点评 本题主要考查二次函数的应用,熟练掌握解直角三角形和解方程的能力求出所需线段的长度及割补法求三角形的面积是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 16000元 | B. | 18000元 | C. | 20000元 | D. | 22000元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
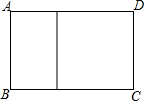 如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).
如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com