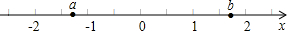Question

附加题（1）已知有理数a、b在数轴上的位置如图所示，请判断下列各式的符号：
 a+b______0； a-b______0；ab______0；
（2）化简：|a+b|+|b-2|-|b-a|+|a-b|；
（3）x是数轴上的一个数，试讨论：x为有理数时，|x-2|+|x+1|是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

Answer 1

解：（1）根据题意得：a＜-1＜0＜1＜b，
∴a+b＞0；a-b＜0；ab＜0；
故答案为：＞，＜，＜；

（2）∵a+b＞0，b-2＜0，b-a＞0，a-b＜0，
∴原式=（a+b）+2-b-（b-a）-（a-b）
=a+b+2-b-b+a-a+b
=a+2；

（3）∵|x-2|和|x+1|都为非负数，
∴只有当其中一个值为0时，才为最小值，
∴当|x-2|=0时，x=2，原式=3；
当|x+1|=0时，x=-1，原式=3；
∴最小值为3．
分析：（1）根据数轴上点的位置判断出各式的正负即可；
（2）根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，去括号合并即可得到结果；
（3）原式两项都为非负数，值要最小，只有一个为0才可以取最小值，即可确定出这个最小值．
点评：此题考查了绝对值，数轴，以及有理数的大小比较，弄清题意是解本题的关键．