
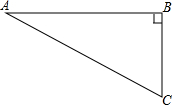
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是$\frac{\sqrt{3}}{6}$. 分析 设BC=x,由含30°角的直角三角形的性质得出AC=2BC=2x,求出AB=$\sqrt{3}$x,根据题意得出AD=BC=x,AE=DE=AB=$\sqrt{3}$x,作EM⊥AD于M,由等腰三角形的性质得出AM=$\frac{1}{2}$x,在Rt△AEM中,由三角函数的定义即可得出结果.
解答 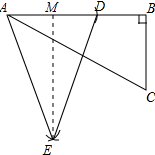 解:如图所示,设BC=x,
解:如图所示,设BC=x,
∵在Rt△ABC中,∠B=90°,∠A=30°,
∴AC=2BC=2x,AB=$\sqrt{3}$BC=$\sqrt{3}$x,
根据题意得:AD=BC=x,AE=DE=AB=$\sqrt{3}$x,
如图,作EM⊥AD于M,则AM=$\frac{1}{2}$AD=$\frac{1}{2}$x,
在Rt△AEM中,cos∠EAD=$\frac{AM}{AE}$=$\frac{\frac{1}{2}x}{\sqrt{3}x}$=$\frac{\sqrt{3}}{6}$,
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查了解直角三角形、含30°角的直角三角形的性质、等腰三角形的性质、三角函数的综合应用,通过作辅助线构造直角三角形,求出AM是解决问题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
 为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )
为避免粉尘污染,某校决定对校内所有教室的黑板(样式相同)进行无尘专用膜升级改造,另配备若干盒无尘粉笔,经过测算,对教室内一块黑板进行无尘专用膜升级改造,再配备一盒无尘粉笔共需180元,该校升级改造65块黑板,并配备45盒无尘粉笔共需10100元,设一块黑板进行无尘专用膜升级改造需x元,配备一盒无尘粉笔需y元,下列方程组正确的是( )| A. | $\left\{\begin{array}{l}{x+45y=180}\\{65x+y=10100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{45x+y=180}\\{x+65y=10100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=180}\\{65x+45y=10100}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{45x+65y=10100}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
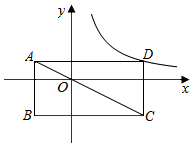 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.
如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上.若点B的坐标为(-2,-2),则k=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
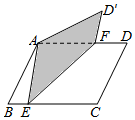 如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.
如图,?ABCD中,∠B=60°,AB=3,BC=4,折叠?ABCD使C落在A处,折痕为EF,点E、F分别在BC、AD上,则AF=$\frac{13}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
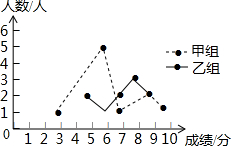 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.8 | a | 3.76 | 90% | 30% |
| 乙组 | b | 7.5 | 1.96 | 80% | 20% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com