
【题目】如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①BD=DC;②AE∥BC;③AE=AG;④AG=![]() DE.正确的是_____(填写序号)
DE.正确的是_____(填写序号)
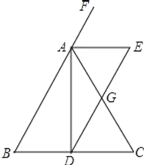
【答案】①②④
【解析】
根据等腰三角形的性质与判定、平行线的性质分别对每一项进行分析判断即可.
解:①∵△ABC中,AB=AC,AD是∠BAC的平分线,
∴BD=DC,
故本选项正确,
②∵△ABC中,AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,
∴AE∥BC,
故本选项正确,
③∵AE∥BC,
∴∠E=∠EDC,
∵ED∥AB,
∴∠B=∠EDC,∠AGE=∠BAC,
∴∠B=∠E,
∵∠B不一定等于∠BAC,
∴∠E不一定等于∠AGE,
∴AE不一定等于AG,
故本选项错误,
④∵ED∥AB,
∴∠BAD=∠ADE,
∵∠CAD=∠BAD,
∴∠CAD=∠ADE,
∴AG=DG,
∵AE∥BC,
∴∠EAG=∠C,
∵∠B=∠E,∠B=∠C,
∴∠E=∠C,
∴∠EAG=∠E,
∴AG=EG,
∴AG=![]() DE,
DE,
故答案为:①②④


科目:初中数学 来源: 题型:
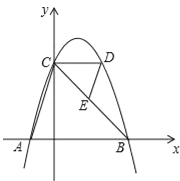
【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线于另一点D,连结AC,DE∥AC交边CB于点E.
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
(1)求这个二次函数的解析式;
(2)若二次函数的图象与x轴交于另一点B,与直线y=x+m交于另一点D,求 △ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是学习分式方程应用时,老师板书的问题和两名同学对该题的解答.(老师找聪聪和明明分别用不同的方法解答此题)

(1)聪聪同学所列方程中的![]() 表示_______________________________________.
表示_______________________________________.
(2)明明一时紧张没能做出来,请你帮明明完整的解答出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
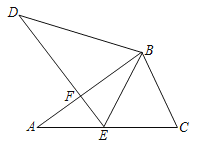
【题目】如图,已知∠A=∠D,AB=DB,点E在AC边上,∠AED=∠CBE,AB和DE相交于点F.
(1)求证:△ABC≌△DBE.
(2)若∠CBE=50°,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
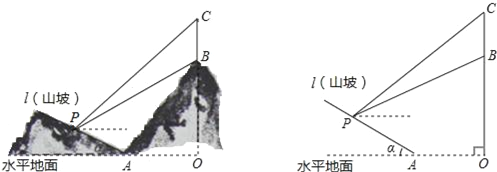
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB切⊙O于A、B,点C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是_____.
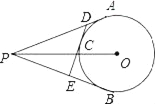
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
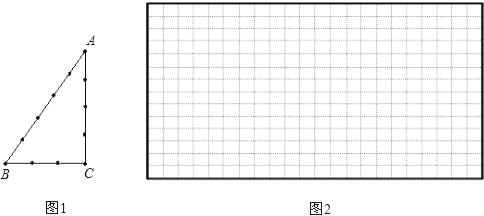
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)
A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方
B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形
(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数
(3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
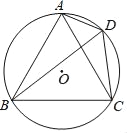
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com