
【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A. 1个B. 2个C. 3个D. 4个
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长 . 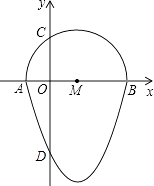
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯承包了一个四边形的池塘,如图所示,它的四个角A,B,C,D处均有一棵大树,张大伯今年养鱼喜获丰收,明年准备把池塘面积扩大一倍,但又不想毁掉这四棵大树,并且扩建后的池塘呈平行四边形形状.张大伯这一设想是否能实现?请你帮助他解决一下,并画出草图.
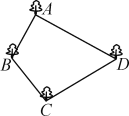
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“中小学生每天锻炼1小时”的号召,某校开展了形式多样的“阳光体育”活动,小明对某班同学参加锻炼的情况进行了调查与统计,并绘制了下面的图1与图2.根据你对图1与图2的理解,回答下列问题:
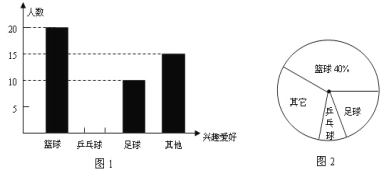
(1)小明调查的这个班级有多少名学生,参加足球锻炼的学生人数所占的百分比是多少?
(2)请你将图1中“乒乓球”部分补充完整.
(3)求出扇形统计图中表示“足球”的扇形的圆心角的度数.
(4)若这个学校共有1200名学生,估计参加乒乓球活动的学生有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
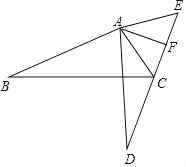
【题目】如图,∠BAD=∠CAE,AB=AD,AC=AE.且E,F,C,D在同一直线上.
(1)求证:△ABC≌△ADE;
(2)若∠B=30°,∠BAC=100°,点F是CE的中点,连结AF,求∠FAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
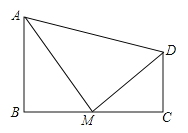
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好地推进太原市生活垃圾分类工作,改善城市生态环境,2019年12月17日,太原市政府召开了太原市生活垃圾分类推进会,意味着太原垃圾分类战役的全面打响.某小区准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该小区物业计划用不多于2100元的资金购买A、B两种型号的垃圾箱共20个,则该小区最多可以购买B型垃圾箱多少个?
(3)在(2)的条件下,要求至少购买3个B型垃圾箱,请设计出最省钱的购买方案,并求出最少购买费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com