
【题目】陈老师要为他家的长方形餐厅(如图1)选择一张餐桌,并且想按如下要求摆放:餐桌一侧靠墙,靠墙对面的桌边留出宽度不小于80 cm的通道,另两边各留出宽度不小于60 cm的通道.那么在图2的四张餐桌中,其规格符合要求的餐桌编号是________.

图1 图2
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分別在线段BC、CD上,∠EAF=30°,连接EF. 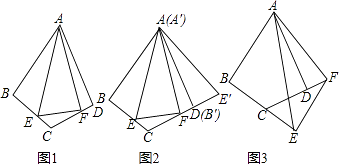
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),那么
①∠E′AF度数②线段BE、EF、FD之间的数量关系
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图所示的一张平行四边形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
(1)求证:四边形AFCE是菱形.
(2)若AB=8cm,∠B=90°,△ABF的面积为24cm2,求菱形AFCE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5……按此规律进行下去,则点A3的坐标为________,点A2017的横坐标为________.
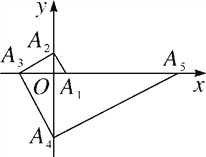
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线AB经过点A(0,3)点B( ![]() ,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C.
,0),点M在y轴上,⊙M经过点A、B,交x轴于另一点C. 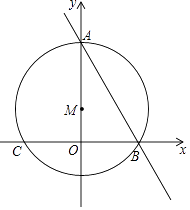
(1)求直线AB的解析式;
(2)求点M的坐标;
(3)点P是劣弧AC上一个动点,当P点运动时,问:线段PA,PB,PC有什么数量关系?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上来回巡逻,一天早晨,他从岗亭出发,中午停留在![]() 处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
处,规定向北方向为正,当天上午连续行驶情况记录如下(单位:千米):+5,﹣4,+3,﹣7,+4,﹣8,+2,﹣1.
(1)![]() 处在岗亭何方?距离岗亭多远?
处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油![]() 升,这一天上午共耗油多少升?
升,这一天上午共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
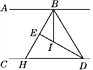
【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com