
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.

(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
【答案】(1) 20°;(2) 35°;
(3)规律:∠NMB=![]() ∠A.
∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
解:(1)∵AB=AC,
∴∠ABM=∠ACB.
∵∠BAC=40°,∠ABM=∠ACB,
∴∠ABM=![]() ×(180°-∠BAC)=70°.
×(180°-∠BAC)=70°.
∵MN是AB的垂直平分线,∠ABM=70°,
∴∠NMB=90°-∠ABM=90°-70°=20°.
(2)与(1)同理可得∠B=![]() ×(180°-∠BAC)=55°,
×(180°-∠BAC)=55°,
∴∠NMB=90°-55°=35°.
(3)规律:在等腰△ABC中,当AB=AC,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.理由如下:
∠A.理由如下:
∵AB=AC,
∴∠ABM=∠ACB.
∴∠ABM=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∵∠ABM=90°-![]() ∠A,∠BNM=90°,
∠A,∠BNM=90°,
∴∠BMN=90°-∠ABM=![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
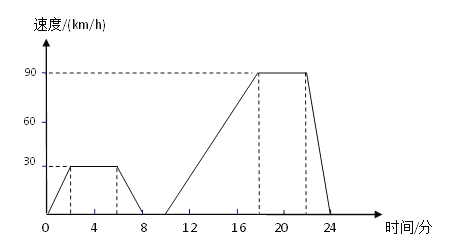
【题目】如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在那些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年我国大学生毕业人数将达到7 490 000人,这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×105
D.0.749×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4根小木棒,长度分别为3cm、5cm、7cm、9cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是
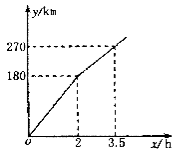
A. 汽车在高速公路上行驶速度为100km/h
B. 乡村公路总长为90km
C. 汽车在乡村公路上行驶速度为60km/h
D. 该记者在出发后4.5h到达采访地
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com