
【题目】如图,直线AB和直线CD相交于点O,OF平分∠COE,过点O作OG⊥OF.

(1)若∠AOE=80°,∠COF=22°,则∠BOD= ;
(2)若∠COE=40°,试说明:OG平分∠DOE.
【答案】(1)36;(2)见解析
【解析】
(1)根据∠COF和∠AOE的度数和OF平分∠COE,求出∠AOC的度数,利用对顶角的性质得出∠BOD的人度数;
(2)根据∠COE=40°的度数求出∠EOG,再根据平角的度数求出∠AOC+∠BOG的度数之和,即∠DOG的度数,根据度数相等即可证明.
解:(1)∵∠COF=22°,OF平分∠COE,
∴∠EOF=22°,
∵∠AOE=80°,
∴∠AOC=80-22°×2=36°,
∴∠BOD=36°;
(2)∵∠COE=40°,OF平分∠COE,
∴∠COF=∠EOF=20°,
∵OG⊥OF,∴∠FOG=90°,
∴∠EOG=70°,∠COF+∠DOG=90°,
∴∠GOD=70°,
∴OG平分∠DOE.


科目:初中数学 来源: 题型:
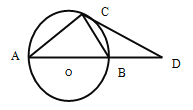
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
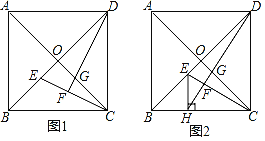
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,
①若△ABC是以BC为斜边的直角三角形,求k的值.
②若△ABC是等腰三角形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有450名学生,随机抽取其中的若干名学生,根据这些学生两次数学模拟考试成绩,分别绘制了如下所示的频数分布直方图,其中图②不完整.

注:① 成绩均为整数;②“60以下”不含60,其余分数段均包含端点;③ 图①、图②分别表示第一次、第二次模拟考试成绩频数分布直方图.
根据以上信息,解答下列问题:
(1)把图②补全;
(2)规定100分以上为优秀,请计算图②中达到优秀的比例;
(3)请你估算九年级学生第二次数学模拟考试达到优秀的人数比第一次数学模拟考试增加多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() .
.
(1)请以AB、BC为邻边用两种不同的方法画平行四边形ABCD,并说明此画法的合理性(不写作法,保留作图痕迹.);
(2)在上述画出的平行四边形中,若![]() ,
,![]() ,
,![]() ,求对角线BD的长.
,求对角线BD的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2017年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆.
(1)若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车?
(2)考虑到自行车需求不断增加,该商城准备投入3万元再购进一批两种规格的自行车,已知A型车的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆.根据销售经验,A型车不少于B型车的2倍,但不超过B型车的2.8倍.假设所进车辆全部售完,为使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
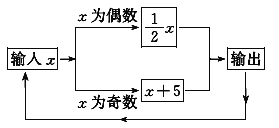
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是__________,依次继续下去……第2 016次输出的结果是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
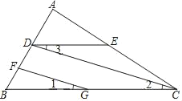
(1)如图,FG∥CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG∥CD(已知)
∴∠2=
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC∥
∴∠B+ =180°
又∵∠B=50°
∴∠BDE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com